Circular objects have numerous applications in practical situations, the use of pulleys and gears in mechanical systems support the operation of various industrial machines and car engines and trucks. The circular movements are transmitted to each other through two standard procedures: leaning against or connected by straps.
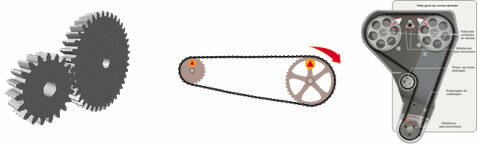
Transmission through gears
In both forms of transmission, the gears have teeth that fit together by contact or in the links of the transmission chain, in order to avoid slipping. The relationship between the number of turns between the gears depends on the radius measurement. If one gear has a radius three times greater than the radius of the other, it means that when it makes a complete turn, the smallest gear will turn three times.
Example 1
Two pulleys A and B with a radius measuring 10 cm and 4 cm are connected by means of a timing belt. How many turns does the smallest pulley make when the largest turns 12 times?
Resolution:
Let's calculate the length of the two pulleys.
Pulley A
C = 2 * π * r
C = 2 * 3.14 * 10
C = 62.8 cm
Pulley B
C = 2 * π * r
C = 2 * 3.14 * 4
C = 25.12
Calculating the ratio between the length of the two pulleys:
length of A / length of B
62,8 / 25,12 = 2,5
When pulley A makes one full turn, pulley B makes 2.5 turns (two full turns plus half a turn). This way, when pulley A rotates 12 times, pulley B will make 30 complete turns, because: 12 * 2.5 = 30.
Example 2
The motor of a sugarcane mill has a pulley with a radius measuring 6 cm. This motor is responsible for turning the mill that is coupled to a pulley with a radius measuring 42 cm. In this case, the transmission is made by a rubber timing belt. How many turns does the smaller pulley need to make for the larger pulley to make a complete turn?
Length of the smaller pulley
C = 2 * π * r
C = 2 * 3.14 * 6
C = 37.68 cm
Length of the longest pulley
C = 2 * π * r
C = 2 * 3.14 * 42
C = 263.76
Ratio between pulleys
263,76 / 37,68 = 7
The smaller pulley needs to make 7 turns for the larger one to make a complete turn.
Do not stop now... There's more after the advertising ;)
by Mark Noah
Graduated in Mathematics
Brazil School Team
Circumference - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Ratio between Circular Movements"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/razao-entre-movimentos-circulares.htm. Accessed on June 28, 2021.