The sector of a circle is a region bounded by two straight line segments that run from the center to the circumference. These line segments are the radii of the circle, see the figure: 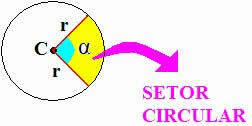
Angle α is called the central angle.
Thus, we realize that the circular sector is a part of the circular region, that is, it is a fraction of the circle's area. Thus, we can say that the area of the circular sector is directly proportional to the value of α, since the area of the entire circle is directly proportional to 360º.
So we can set up the following relationship (rule of three):
Sector area α
360° circle area
Sector = α
πr² 360°
Sector 360° = α. πr²
Asector = α. πr²
360°
Example: Determine the area of the circular sector of radius 6cm whose central angle measures:
• 60°
Sector = 60°. π6²
360°
Sector = 60°. π 36
360°
Sector = 6π cm²
• π/2
π/2 corresponds to 90°
Sector = 90°. π6²
360°
Sector = 90°. π36
360°
Sector = 9π cm²
Do not stop now... There's more after the advertising ;)
by Danielle de Miranda
Graduated in Mathematics
Brazil School Team
Spatial Metric Geometry -Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
DANTAS, James. "Circular sector area"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/area-setor-circular.htm. Accessed on June 27, 2021.



