The circle has some important metric relationships involving inner segments, secants, and tangents. Through these relationships we obtain the measures sought.
Crossing between two strings
The crossing of two chords on the circumference generates proportional segments, and the multiplication between the measurements of the two parts of one string is equal to the multiplication of the measurements of the two parts of the other rope. Watch:

AP * PC = BP * PD
Example 1

x * 6 = 24 * 8
6x = 192
x = 192/6
x = 32
Two secant segments starting from the same point
In any circumference, when we draw two secant segments, starting from the same point, the multiplication of the measure of one of them by the measure of its outer part is equal to the multiplication of the measure of the other segment by the measure of its part. external. Watch:
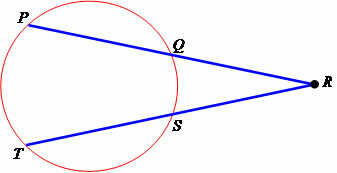
RP * RQ = RT * RS
Example 2

Do not stop now... There's more after the advertising ;)
x * (42 + x) = 10 * (30 + 10)
x2 + 42x = 400
x2 + 42x – 400 = 0
Applying the solving form of a 2nd degree equation:
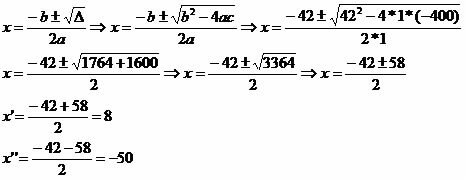
The results obtained are x’ = 8 and x’’ = – 50. As we are working with measures, we should only consider the positive value x = 8.
Secant segment and tangent segment starting from the same point
In this case, the square of the measure of the tangent segment is equal to the multiplication of the measure of the secant segment by the measure of its outer part.

(BECAUSE)2 = PS * PR
Example 3

x2 = 6 * (18 + 6)
x2 = 6 * 24
x2 = 144
√x2 = √144
x = 12
by Mark Noah
Graduated in Mathematics
Brazil School Team
Circumference - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Metric Relationships Concerning Circumference"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/relacoes-metricas-referentes-circunferencia.htm. Accessed on July 27, 2021.

