Quadratic Function Calculation

THE quadratic function, also called 2nd degree polynomial function, is a function represented by the following expression:

f(x) = ax² + bx + c

Where The, B and ç are real numbers and The ≠ 0.

Example:

f (x) = 2x² + 3x + 5,

being,

a = 2
b = 3
c = 5

In this case, the quadratic function polynomial is of degree 2, as it is the largest exponent of the variable.

How to solve a quadratic function?

Check out the step by step through an example of solving the quadratic function:

Example

Find a, b and c in the quadratic function given by: f (x) = ax² + bx + c, being:

f(-1) = 8
f (0) = 4
f(2) = 2

First, let's replace the x by the values ​​of each function and thus we will have:

f(-1) = 8
to 1)² + b (–1) + c = 8
a - b + c = 8 (equation I)

f (0) = 4
The. 0² + b. 0 + c = 4
c = 4 (equation II)

f(2) = 2
The. 2² + b. 2 + c = 2
4a + 2b + c = 2 (equation III)

By the second function f (0) = 4, we already have the value of c = 4.

So, let's substitute the obtained value for ç in equations I and III to determine the other unknowns (The and B):

(Equation I)

a - b + 4 = 8
a - b = 4
a = b + 4

Since we have the equation of The by Equation I, let's substitute in III to determine the value of B:

(Equation III)

4a + 2b + 4 = 2
4a + 2b = - 2
4 (b + 4) + 2b = - 2
4b + 16 + 2b = - 2
6b = - 18
b = - 3

Finally, to find the value of The we replace the values ​​of B and ç that have already been found. Soon:

(Equation I)

a - b + c = 8
a - (- 3) + 4 = 8
a = - 3 + 4
a = 1

Therefore, the coefficients of the given quadratic function are:

a = 1
b = - 3
c = 4

Roots of Function

The roots or zeros of the second degree function represent the values ​​of x such that f(x) = 0. The roots of the function are determined by solving the second degree equation:

f(x) = ax² +bx + c = 0

To solve the 2nd degree equation we can use several methods, one of the most used is applying the Bhaskara formula, i.e:

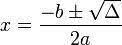
Example

Find the zeros of the function f (x) = x² – 5x + 6.

Solution:

Being
a = 1
b = – 5
c = 6

Substituting these values ​​in Bhaskara's formula, we have:

So the roots are 2 and 3.

Note that the number of roots of a quadratic function will depend on the value obtained by the expression: Δ = b² – 4. B.C, which is called the discriminant.

Thus,

• if Δ > 0, the function will have two real and distinct roots (x₁ ≠ x₂);
• if Δ, the function will not have a real root;
• if Δ = 0, the function will have two real and equal roots (x₁ = x₂).

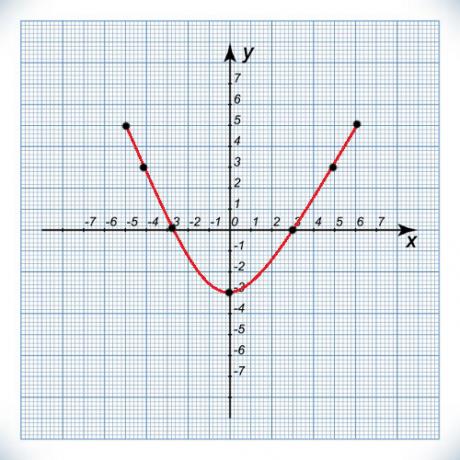
Graph of the quadratic function

The graph of 2nd degree functions are curves that are called parabolas. different from 1st degree functions, where knowing two points it is possible to draw the graph, in quadratic functions it is necessary to know several points.

The curve of a quadratic function cuts the x-axis at the roots or zeros of the function, at a maximum of two points depending on the value of the discriminant (Δ). So we have:

• If Δ > 0, the graph will cut the x axis at two points;
• If Δ
• If Δ = 0, the parabola will touch the x-axis at only one point.

There is yet another point, called the vertex of the parabola, which is the maximum or minimum value of the function. This point is found using the following formula:

The vertex will represent the maximum value point of the function when the parabola is facing downwards and the minimum value when facing upwards.

It is possible to identify the position of the concavity of the curve by analyzing only the sign of the coefficient The. If the coefficient is positive, the concavity will be facing upwards and if it is negative, it will be downwards, that is:

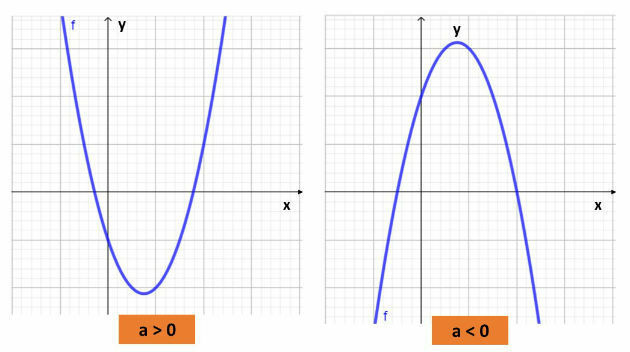
So, to sketch the graph of a 2nd degree function, we can analyze the value of The, calculate the function's zeros, its vertex and also the point where the curve cuts the y axis, that is, when x = 0.

From the given ordered pairs (x, y), we can construct the parabola num Cartesian plane, through the connection between the points found.

Entrance Exam Exercises with Feedback

1. (Vunesp-SP) All possible values ​​of m that satisfy the 2x inequality² – 20x – 2m > 0, for all x belonging to the set of reais, are given by:

a) m > 10
b) m > 25
c) m > 30
d) m e) m

See Answer

Alternative b) m > 25

2. (EU-CE) The graph of the quadratic function f (x) = ax² + bx is a parabola whose vertex is the point (1, – 2). The number of elements of the set x = {(– 2, 12), (–1,6), (3,8), (4, 16)} that belong to the graph of this function is:

to 1
b) 2
c) 3
d) 4

See Answer

Alternative b) 2

3. (Cefet-SP) Knowing that the equations of a system are x. y = 50 and x + y = 15, the possible values ​​for x and y they are:

a) {(5.15), (10.5)}
b) {(10.5), (10.5)}
c) {(5.10), (15.5)}
d) {(5.10), (5.10)}
e) {(5.10), (10.5)}

See Answer

Alternative e) {(5.10), (10.5)}

Read too:

• First Degree Equation
• Second degree equation
• Related Function Exercises
• High School Equation - Exercises
• Modular Function
• Exponential Function
• Polynomial Function
• Composite Function
• Injector Function
• Bijector Function
• Overjet Function
• inverse function
• Quadratic Function - Exercises
• Polynomials
• Polynomial Factoring
• Exponential Function - Exercises
• Mathematics in Enem
• Math Formulas