We established a occupation when we relate one or more quantities. Part of natural phenomena can be studied thanks to the development in this area of mathematics. The study of functions is divided into two parts, we have the general part, in which we study the conceptsgeneral, and the specific part, where we study the particular cases, such as polynomial functions and exponential functions.
See too: How to graph a function?
What are functions?
A function is an application that relates the elements of two sets not empty. Consider two non-empty sets A and B, where a function f relate each element from A to only one element of B.
To better understand this definition, imagine a taxi ride. For each trip, that is, for each distance covered, there is a different and unique price, that is, it makes no sense for a trip to have two different prices.
We can represent this function that takes elements from set A to set B in the following ways.

Note that for each element of set A, there is a single related element
with him in set B. Now we can think, after all, when a relationship between two sets will not be a function? Well, when an element of the set A is related to two distinct elements of B, or when there are elements of the set A that are not related to elements of B. Look:
Generally speaking, we can write a function algebraically like this:
f: A → B
x → y
Note that the function takes elements from set A (represented by x) and takes them to elements of B (represented by y). We can also say that the elements of set B are given in terms of the elements of set A, so we can represent y by:
y = f(x)
It reads: (y equals f of x)

Domain, co-domain and image of a role
When we have a role f, the sets being related are given special names. So consider a function f which takes elements from set A to elements from set B:
f: A → B
Do not stop now... There's more after the advertising ;)
The set A, from which the relations depart, is called domain of the function, and the set that receives the "arrows" of this relationship is called counter-domain. We denote these sets as follows:
Df = A → Domain of f
CDf = B → Counterdomain of f
The subset of the counterdomain of a function formed by elements that relate to elements of the set is called Image of the function and is denoted by:
imf → Image of f
- Example
Consider the function f: A → B represented in the diagram below and determine the domain, the counterdomain, and the image.
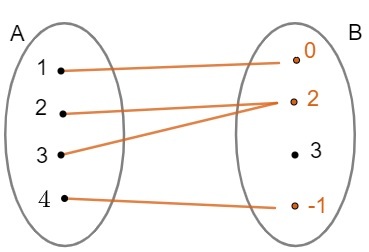
As said, the set A = {1, 2, 3, 4} is the domain of the function f,while the set B = {0, 2, 3, –1} is the counterdomain of the same function. Now, notice that the set formed by elements that receive the arrow (in orange) formed by the elements {0, 2, –1} is a subset of the counterdomain B, this set is the image of the function f, thus:
Df = A = {1, 2, 3, 4}
CDf = B = {0, 2, 3, -1}
imf = {0, 2, –1}
We say that the 0 is element image 1 of the domain, as well as the 2 it's image of the elements 2 and 3 of the domain, and –1 is element image 4 of the domain. To learn more about these three concepts, read: Ddomain, co-domain and image.
Surjective function
A function f: A → B will be surjective or surjective if, and only if, the image set coincides with the contradomain, that is, if all elements of the contradomain are images.
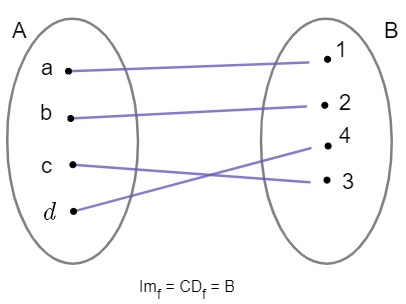
We say then that a function is surjective when all elements of the counterdomain receive arrows. If you want to go deeper into this type of function, visit our text: Overjet function.
Injective function
A function f: A → B will be injective or injective if, and only if, distinct elements of the domain have distinct images in the counterdomain, that is, like images are generated by like elements of the domain.

Note that the condition is that different elements of the domain relate to different elements of the counterdomain, there being no problem with remaining elements in the counterdomain. To better understand this concept, you can read the text: Injector function.
Bijector function
A function f: A → B will be bijective if, and only if, it is injector and surjector simultaneously, that is, distinct elements of the domain have distinct images, and the image coincides with the counter-domain.
- Example
In each case, justify whether the function f (x) = x2 it is injector, surjector or bijector.
The) f: ℝ+ → ℝ
Note that the function's domain is all positive reals and the counterdomain is all real numbers. We know that the function f is given by f (x) = x2, now imagine all the positive real numbers being high squared, all images will also be positive. So we can conclude that the function is injecting and not surjective, since negative real numbers will not receive arrows.
It is injecting, as each element of the domain (ℝ+) relates only to one element of the counterdomain (ℝ).
B) f: ℝ → ℝ+
The function, in this case, has the domain as all reals and the counterdomain as positive reals. We know that any real number squared is positive, so all elements of the counterdomain have received arrows, so the function is surjective. It will not be injecting because domain elements relate to two counter-domain elements, for example:
f(–2) = (–2)2 = 4
f(2) = (2)2 = 4
ç) f:ℝ+ → ℝ+
In this example the function has domain and counterdomain as the positive real numbers, so the function is bijector, because each positive real number relates to a single real number positive of the counterdomain, in this case the square of the number. In addition, all counterdomain numbers received arrows.
composite function
THE composite function is associated with the shortcut idea. Consider three non-empty sets A, B and C. Also consider two functions f and g, where function f takes elements x from set A to elements y = f (x) from set B, and function g takes elements y = f (x) to elements z from set C.
The composite function receives this name because it is an application that takes elements from set A directly to elements from set C, without going through set B, through the composition of functions f and g. Look:

The function denoted by (f o g) takes the elements from set A directly to set C. It is called a composite function.
- Example
Consider the function f(x) = x2 and the function g (x) = x + 1. Find the composite functions (f o g)(x) and (g o f)(x).
The function f o g is given by the function g applied to f, that is:
(f o g)(x) = f (g(x))
To determine this composite function, we must consider the function f,and, in place of the variable x, we must write the function g. Look:
x2
(x+1)2
(f o g)(x) = f (g(x)) = x2 + 2x + 1
Similarly, to determine the composite function (g o f)(x), we must apply the function f in the role g, that is, consider the function g and write the function f in place of the variable. Look:
(x + 1)
x2 + 1
Therefore, the composite function (g o f)(x) = g (f (x)) = x2 + 1.
Even function
Consider a function f: A → ℝ, where A is a subset of the non-empty reals. A function f will be even only for all real x.

Example
Consider the function f: ℝ → ℝ, given by f (x) = x2.
Note that for any real x value, if squared, the result is always positive, that is:
f(x) = x2
and
f(–x) = (–x)2 = x2
So f(x) = f(–x) for any real x value, so the function f it's pair.
Read too:Power propertiess - what are they and how at useair?
unique function
Consider a function f: A → ℝ, where A is a subset of the non-empty reals. A function f will be odd only for all real x.
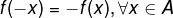
- Example
Consider the function f: ℝ → ℝ, given by f (x) = x3.
See that for any value of x we can write that (–x)3 = -x3. Check out some examples:
(–2)3 = –23 = –8
(–3)3 = –33 = –27
So we can say that:
f(–x) = (–x)3 = –x3
f(–x) = (–x)3 = –f(x)
So for any real x f(–x) = –f (x), and so the function f (x) = x3 is unique.
increasing function
A function f é growing at an interval if and only if, as domain elements grow, their images also grow. Look:

Note that x1 > x2 and the same happens with the image, so we can establish an algebraic condition for the function f be growing.

Descending function
A function f é decreasing at an interval if and only if, as the domain elements grow, their images decrease. Look:
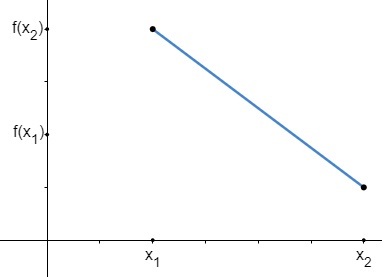
See that, in the function domain, we have that x1 > x2, however this does not occur in the function image, where f (x1) < f(x2). So we can establish an algebraic condition for decreasing functions. Look:
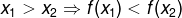
constant function
As the name says, a function is constant when, for any value domain, the value of the image is always the same.
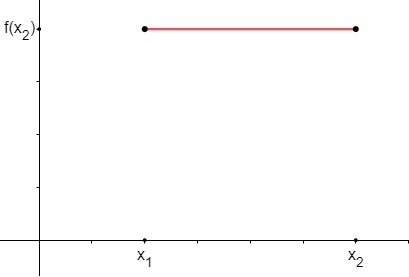
related function
THE affine function or polynomial of the first degree is written in the form:
f (x) = ax + b
Where a and b are real numbers, a is nonzero, and your graph is a line. The function has real domain and also real counterdomain.
quadratic function
THE quadratic function or polynomial function of the second degree is given by a polynomial of grade two, thus:
f(x) = ax2 + bx + c
Where a, b, and c are real numbers with a nonzero, and your graph is a parable. The role also has real domain and counter domain.
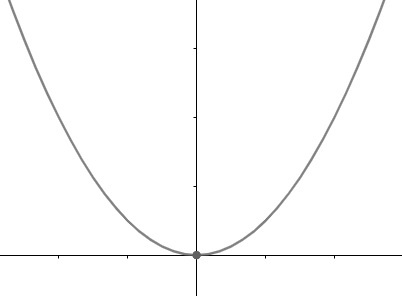
modular function
THE modular function with variable x finds-if inside the module and algebraically it is expressed by:
f(x) = |x|
The function also has real domain and counter domain, that is, we can calculate the absolute value of any real number.

exponential function
THE exponential functiondisplays the variable x in the exponent. It also has real domain and real counterdomain and is described algebraically by:
f(x) = ax
Where a is a real number greater than zero.
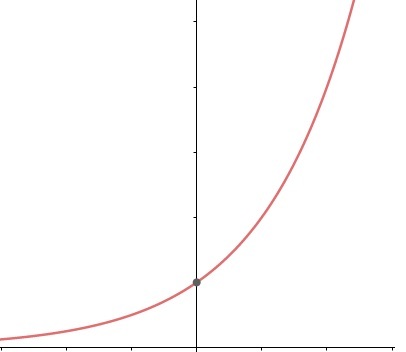
logarithmic function
THE logarithmic function has the variable in logarithm and the domain formed by real numbers greater than zero.


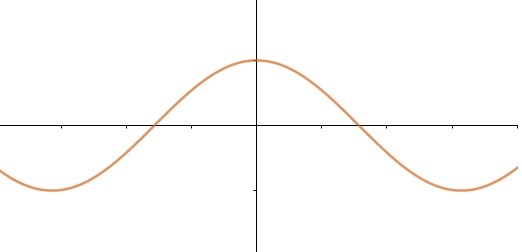
Trigonometric Functions
At trigonometric functions have the variable x involving trigonometric ratios, the main ones are:
f(x) = sin(x)

f(x) = cos(x)
f(x) = tg(x)
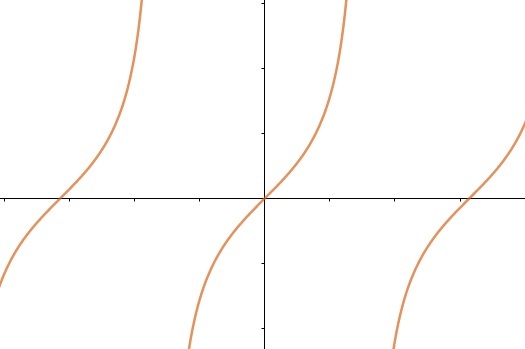
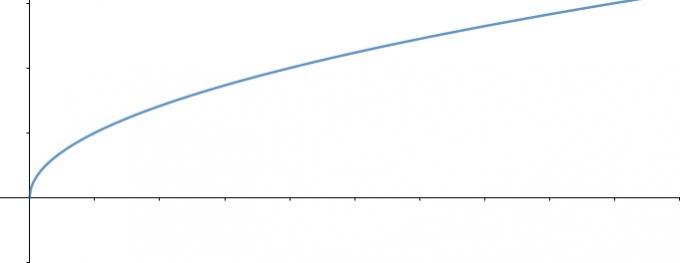
root function
The root function is characterized by having the variable inside the root, thus, if the index of the root is even, the domain of the function becomes only positive real numbers.
by Robson Luiz
Maths teacher
In a metallurgical industry, the production cost of an automotive part corresponds to a fixed monthly cost of R$ 5 000.00 plus a variable cost of R$ 55.00 per unit produced plus 25% tax on the cost variable. Considering that the sale price of this part by the industry to merchants is R$ 102.00, determine:
a) the cost function of producing x pieces.
b) the revenue function referring to the sale of x pieces.
c) the profit function on the sale of x pieces.
BMI (Body Mass Index) is a mathematical function that determines whether an adult person is considered fat, obese, normal or underweight, relating the person's mass in kilograms to the square of the height measurement in meters. According to the table below, determine the mass of a person who is 1.90 meters tall, so that his BMI is considered normal.