At metric relationships at the triangle equilateral registered are expressions which can be used to calculate some of the measurements in this figure using just the measurement of the circle radius.
We say that a polygon it is registered in a circumference when all its vertices belong to it. One triangleequilateral is one that has all congruent sides. As a result of this, all angles of it are also congruent and measure 60°.
From this information, observe the metric relationships in the triangleequilateralregistered.
An inscribed triangle defines three central 120° angles
To realize this, see that the triangleequilateral divide the circumference in three equal parts, as shown in the following figure:
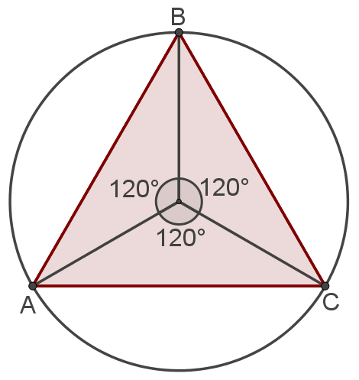
Therefore, each angleinternal is the third part of the complete circumference:
1·360 = 120
3
Side of the inscribed triangle is obtained by the expression:
l = r√3
In this expression, l is the measure on the side of the triangle and r is the measure of lightning gives circumference in which this figure is enrolled.
This expression is obtained from the triangle itself, in which the radius of the circle and the apothem, as done in the following image:
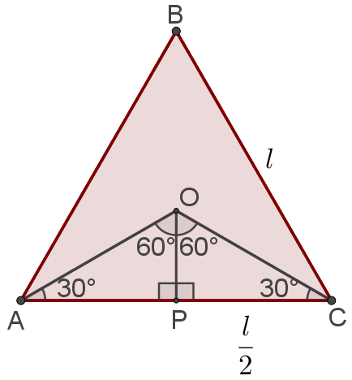
O apothem it is a straight segment starting from the center of a polygon and going to the midpoint of one of its sides. Like this triangle é equilateral, the apothema is also bisector and height of the central angle AÔC.
Do not stop now... There's more after the advertising ;)
We already know, then, that in the triangle built, we have a right angle and a 60° angle, as highlighted in the figure. Furthermore, we also know that the apothema splits the AC side in half. Thus, the segment PC in the figure measures 1/2.
After this procedure, which will also be used in the next relationshipmetric, just look at the POC triangle, highlighted in the image below:

If we calculate the 60° sine in this triangle, we have:
sen60° = 1/2
r
√3 = there 22r
√3 = there
r
r√3 = l
l = r√3
Apothem of the inscribed equilateral triangle is given by the expression:
a = r
2
This expression is obtained from the calculation of the 60° cosine in the POC triangle of the relationshipmetric previous. Calculating cosine of 60°, we have:
cos60° = The
r
1 = The
2 r
r = the
2
Example:
Calculate the lengths of the apothem and on the side of a triangleequilateralregistered on a circumference of radius 20 cm.
Solution: To calculate these measures, just use the formulas given to find out the apothem and the side of triangleequilateral, replacing them with the measure of the radius of the circumference.
Apothem:
a = r
2
a = 20
2
a = 10 cm
Side:
l = r√3
l = 20√3
l = 20·1.73
l = 34.6 cm
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "Metric relations in the inscribed equilateral triangle"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/relacoes-metricas-no-triangulo-equilatero-inscrito.htm. Accessed on June 27, 2021.