At logarithmic inequalities are all those that present logarithms. The unknown, in these cases, is in the logarithm and/or in the base. Remember that one logarithm has the following format:
logThe b = x ↔ ax = b,
*The and the base of logarithm;B it's the logarithm and x it's the logarithm.
To solve logarithmic inequalities, we apply the operative properties of logarithms and the traditional concepts of solving inequalities. Just like we do with logarithmic equations, it is important to check the conditions of existence of the logarithms (both the base and the logarithm must be greater than zero).
By developing the logarithmic inequalities, we can achieve two situations:
1st) Inequality between logarithms on the same basis:
logThe b < logThe ç
Here we have two cases to be analyzed: if the base is greater than 1 (a > 1), we can disregard the logarithm and maintain inequality between the logarithms, that is:
If a > 1 then logThe b < logThe c ↔ b < c
If, on the other hand, the base is a number between 0 and 1 (0 > a > 1)
, when solving the logarithmic inequality, we must reverse inequality and establish an inequality between the logarithms, that is:If 0 > a > 1, then logThe b < logThe c ↔ b > c
2nd) Inequality between a logarithm and a real number:
logThe b < x
If, when solving a logarithmic inequality, we come across an inequality between a logarithm and a real number, we can apply the basic property of the logarithm, keeping the symbol of the inequality:
logThe b < x ↔ b < ax
or
logThe b > x ↔ b > ax
Let's look at some examples of solving logarithmic inequalities:
Example 1: log5 (2x - 3) < log5 x
We must check the conditions of existence of the logarithms:
Do not stop now... There's more after the advertising ;)
2x – 3 > 0 |
x > 0 |
We have an inequality between logarithms of the same base which is bigger than 1. We can then maintain the inequality only between the logarithmans:
log5 (2x - 3) < log5 x
2x – 3
2x - x < 3
x < 3
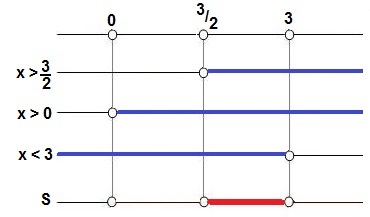
Example 1 resolution chart
In this case, the solution is
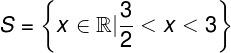
.
Example 2: log2 (x + 3) ≥ 3
First, we check the condition of existence of the logarithm:
x + 3 > 0
x > – 3
In this case, there is an inequality between a logarithm and a real number. We can solve the logarithm in the conventional way, keeping the inequality:
log2 (x + 3) ≥ 3
x + 3≥ 23
x + 3≥ 8
x≥ 8 - 3
x≥ 5
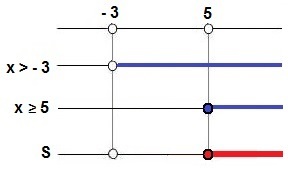
Example 2 resolution chart
The solution is  .
.
Example 3: log1/2 3x > log1/2 (2x + 5)
Checking the conditions of existence of the logarithms, we have:
|
3x > 0 x > 0 |
2x + 5 > 0 2x > – 5 x > – 5/2 |
In this example, there is an inequality between logarithms of the same base which is smaller than1. To solve it, we must invert the inequality, applying it between the logarithmans:
log1/2 3x > log1/2 (2x + 5)
3x < 2x + 5
3x - 2x < 5
x < 5
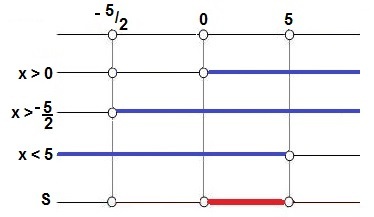
Example 3 resolution chart
In this case, the solution is 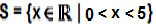 .
.
By Amanda Gonçalves
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
RIBEIRO, Amanda Gonçalves. "Logarithmic inequalities"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/inequacoes-logaritmicas.htm. Accessed on June 28, 2021.
Inequation, what is inequality, signs of inequality, study of the sign, study of the sign of an inequality, product inequality, product of inequalities, function, sign game.