An elementary thought about the position of a point in relation to a circle is that this point can take three different positions. But how to actually verify the position of a point on the Cartesian plane in relation to a circle whose equation we know? For this we will need to calculate the distance from the point to the center of the circle or replace this point in the equation of the circle and analyze the obtained result.
Before starting this algebraic analysis, let's look at the three dot positions:
• The point is inside the circle. This happens only if the distance from the point to the center is smaller than the radius.
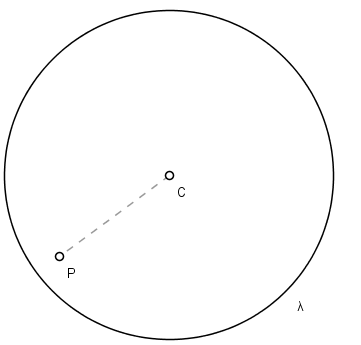
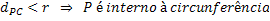
• The point belongs to the circle. This happens if the distance from this point to the center is equal to the radius.
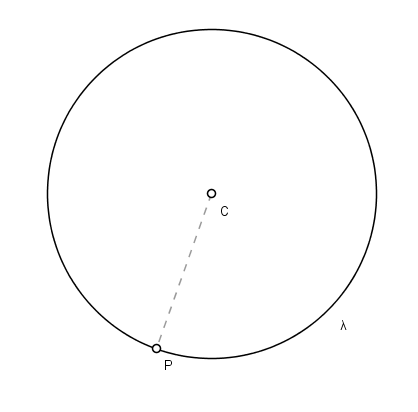
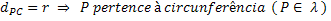
• The point is outside the circle. This occurs when the distance from the point to the center is greater than the radius.

Therefore, when we have to check the relative position of a point with respect to a circle, we must calculate the distance between the center and the point, or substitute the coordinates of the point in the equation of the circle and check the value numerical obtained.
Example:

When the circumference equation is in its reduced form, you don't need to use the distance formula, because the reduced equation gives you the distance of these two points, just solve the left side of the equality and compare the result to the radius (4²).
• Point H (2,3);
Do not stop now... There's more after the advertising ;)
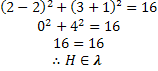
As the distance from point H was equal to the radius, we can say that this point belongs to the circle.
• Point I (3.3);
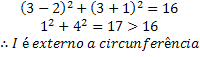
In this case, we equate to 16 expecting the result to be 16 so that the point belongs to the circle, but when performing the calculations we get a value greater than the radius, so the point is outside the circumference.
• Point J (3,2);

But how would we analyze the point if the equation of the circumference came in its general form? The procedure is very similar, however in the general equation we don't have an algebraic expression equal to the radius of the circle. Let's look at the same circle as in the previous example, but written in its general form.

Note that if we take points that belong to the circle, the equation above should equal zero. If not, the point does not belong to the circle. Let's look at the same points from the previous example, but using the general equation:
• Point H (2,3);

As the distance from point H was equal to the radius, we can say that this point belongs to the circle.
• Point I (3.3);
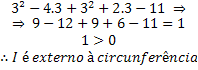
In this case, we equate to 16 expecting the result to be 16 so that the point belongs to the circle, but when performing the calculations we get a value greater than the radius, so the point is outside the circumference.
• Point J (3,2);

By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Gabriel Alessandro de. "Relative positions between a point and a circle"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/posicoes-relativas-entre-ponto-circunferencia.htm. Accessed on June 28, 2021.

