René Descartes must be considered a genius in Mathematics, as he related Algebra to Geometry, the result of this study was the creation of the Cartesian Plan. This merger resulted in Analytical Geometry. Descartes gained great prominence in the fields of Philosophy and Physics, being considered a key player in the Scientific Revolution, and was called the father of modern Mathematics several times. He argued that Mathematics had technical knowledge for the evolution of any area of knowledge.
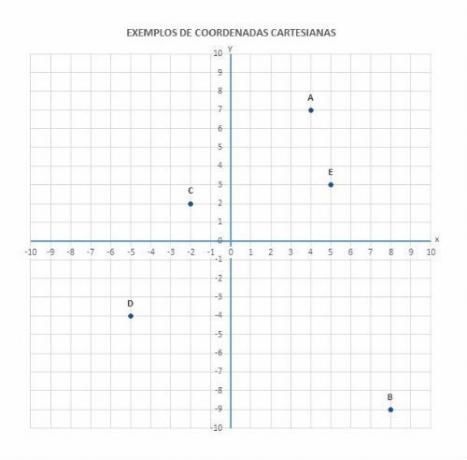
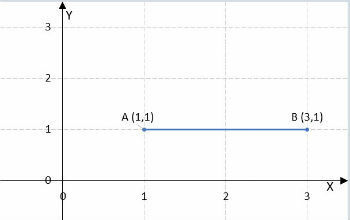
The Cartesian Coordinate System, more commonly known as the Cartesian Plane, consists of two perpendicular axes numbered, called abscissa (horizontal) and ordinate (vertical), which has the characteristic of representing points in space.
Descartes used the Cartesian Plan in order to represent planes, lines, curves and circles through mathematical equations. The initial studies of Analytical Geometry emerged with the theories of René Descartes, which represented geometrical properties numerically. The creation of Analytical Geometry by Descartes was fundamental for the creation of Differential and Integral Calculus by scientists Isaac Newton and Leibniz. The Calculus is dedicated to the study of the rates of variation of quantities and the accumulation of quantities, being of great importance in Physics, Biology and Chemistry, with regard to more complex calculations and detailed.
In addition to Calculus and Analytical Geometry, Descartes' studies allowed the development of Cartography, the science responsible for the mathematical aspects linked to the construction of maps.
Do not stop now... There's more after the advertising ;)
by Mark Noah
Graduated in Mathematics
Brazil School Team
Analytical Geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "The Mathematics of René Descartes (1596 – 1650)"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/a-matematica-rene-descartes-15961650.htm. Accessed on June 28, 2021.