Midpoint of a straight line

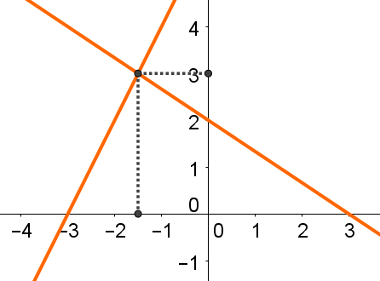
O segmentinstraight has numerous aligned points, but only one of them divides the segment in two equal parts. The identification and determination of the midpoint of a straight segment will be demonstrated based on the following illustration:

O straight segment AB has a midpoint (M) with the following coordinates (x_My_M). Note that the triangles AMN and ABP are similar and have three equal angles. In this way, we can apply the following relationship between the segments that form the triangles. Look:

AM = AN
AB AP

We can conclude that AB = 2 * (AM), considering that M is the Scoreaverage of segment AB.

 AM = AN
2AM AP

AN = 1
AP 2

AP = 2AN

x_P – x_THE = 2*(x_M – x_THE)
x_B – x_THE = 2*(x_M – x_THE)
x_B – x_THE = 2x_M – 2x_THE
2x_M = x_B – x_THE + 2x_THE
2x_M = x_THE + x_B
x_M = (x_THE + x_B)/2

Through an analogous method, we were able to demonstrate that y_M = (y_THE + y_B )/2.

Therefore, considering M o Scoreaverage of segment AB, we have the following mathematical expression to determine the coordinatesofScoreaverage of any segment in the Cartesian plane:

Do not stop now... There's more after the advertising ;)

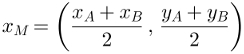
We realize that the calculation of the abscissa x_M and the arithmetic average between the abscissa of points A and B. Thus, the calculation of the y ordinate_M is the arithmetic mean between the ordinates of points A and B.

Examples

→ Given the coordinates of points A(4,6) and B(8,10) belonging to segment AB, determine the coordinates of Scoreaverage of that segment.

X_THE = 4
y_THE = 6
x_B = 8
y_B = 10

x_M = (x_THE + x_B) / 2
x_M = (4 + 8) / 2
x_M = 12/2
x_M = 6

y_M = (y_THE + y_B) / 2
y_M = (6 + 10) / 2
y_M = 16 / 2
y_M = 8

The coordinates of the Scoreaverage of segment AB are x_M (6, 8).

→ Given the points P(5,1) and Q(–2,–9), determine the coordinates of Scoreaverage of the PQ segment.

X_M = [5 + (–2)] / 2
x_M = (5 – 2) / 2
x_M = 3/2

y_M = [1 + (–9)] / 2
y_M = (1 – 9) / 2
y_M = –8/2
y_M = –4

Therefore, M(3/2, –4) is the midpoint of the PQ segment.

by Mark Noah
Graduated in Mathematics

Would you like to reference this text in a school or academic work? Look:

SILVA, Marcos Noé Pedro da. "Midpoint of a straight segment"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/ponto-medio-um-segmento-reta.htm. Accessed on June 28, 2021.