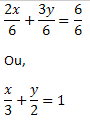One straight it is a set of points that do not curve. In a straight line, there are infinite points, which also indicates that the straight it is infinite. The straight line can also be considered as a space that has only one dimension, that is, it is on the line that figures with one dimension or less are built.
Two straight they can be found at 0, 1 or 2 points. In the first case, they are called parallel; in the second they are called competitors and the meeting point between them is called intersection point; in the third case, if two lines have two points in common, then they must have all points in common and are called coincident.
In the case where two lines have a Scoreinintersection (or intersection), it will always be possible to find the coordinates from that point when the equations of these straight are known.
Coordinates of the intersection point
Suppose the straight ax + by + c = 0 and dx + ey + f = 0 are found in the Score P(xOyO). Note that the unknown values at this point will be the same for both
equations and that this is precisely the definition of a system of equations with two unknowns and two equations. This system can be written as follows:
So, solving this system, we will find the values of x and y that make it true and that, at the same time, are the coordinatesofScore meeting between the two straight that form it.
Example: Determine the meeting point between the lines 2x – y + 6 = 0 and 2x + 3y – 6 = 0
The coordinates of the Scoreinintersection between these two straight are given by solving the formed system:
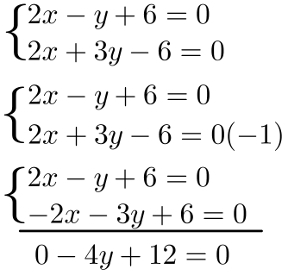
We chose the addition method to solve this system, and this was not done for any particular reason. Continuing with the solution, just resolve the equation found:
– 4y + 12 = 0
Do not stop now... There's more after the advertising ;)
– 4y = – 12 (– 1)
4y = 12
y = 12
4
y = 3
Finally, we can substitute the value of y in any of the equations:
2x - y + 6 = 0
2x – 3 + 6 = 0
2x + 3 = 0
2x = – 3
x = – 3
2
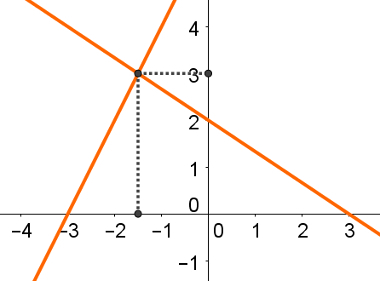
Thus, the coordinates of the intersection between these two straight are: (3, – 3/2).
Note the two straight lines and your Scoreinmeeting in the following graphic:
Simplified solution
The above solution is given when the equations are in your general form. If the equations are given in your reduced form, the solution can be done by another method, with easier and faster calculations. We can also write the equations in its reduced form before doing the calculations to avoid solving the system.
The simplified solution consists of isolating one of the unknowns from the equations and match your results. For example, determine the coordinates of the lines of equations: x + y – 2 = 0 and 3x – y + 4 = 0.
Isolating one unknown from each of them:
y = 2 - x and
y = 4 + 3x
Note that both expressions as a function of x are equal to y. Since both are equal to the same number, then the expressions are equal to each other:
2 - x = 4 + 3x
– x – 3x = 4 – 2
– 4x = 2
x = - 2
4
x = - 1
2
Substituting the value of x in one of the equations, we will find the value of y:
y = 2 - x
y = 2 - 1
2
y = 4 – 1
2
y = 3
2
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "Intersection point between two straight lines"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/ponto-intersecao-entre-duas-retas.htm. Accessed on June 28, 2021.
Point, line, Cartesian plane, slope, fundamental equation of the line, how to find the fundamental equation of the line, what is fundamental equation of the line, demonstration of the fundamental equation of the straight.