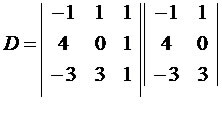Hyperbole. definition of hyperbole

What is hyperbole?
Definition: Let F1 and F2 be two points on the plane and let 2c be the distance between them, hyperbola is the set of the points in the plane whose difference (in module) of the distances to F1 and F2 is the constant 2a (0 < 2a < 2c).
Elements of a Hyperbole:

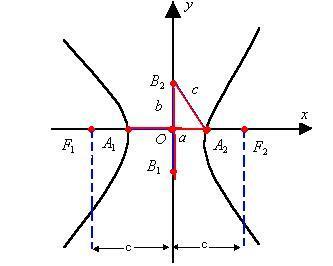
F1 and F2 → are the foci of hyperbola
→ is the center of hyperbole
2c → focal length
2nd → real or transverse axis measurement
2b → imaginary axis measurement
c/a → eccentricity
There is a relationship between a, b and c → c² = the² + b²

Reduced hyperbola equation
1st case: Hyperbola with focuses on the x axis.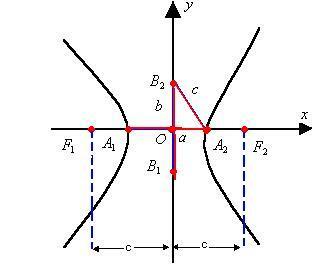

It is clear that in this case the foci will have coordinates F1 (-c, 0) and F2(c, 0).
Thus, the reduced equation of the ellipse with center at the origin of the Cartesian plane and focuses on the x axis will be: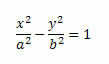

2nd case: Hyperbola with focuses on the y axis.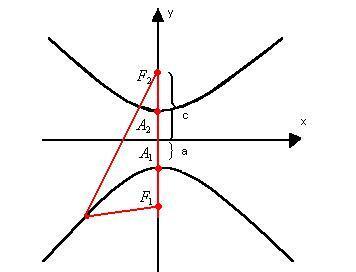

In this case, the foci will have coordinates F1 (0, -c) and F2(0, c).
Thus, the reduced equation of the ellipse with center at the origin of the Cartesian plane and focuses on the y axis will be:

Example 1. Find the reduced equation of the hyperbola with real axis 6, foci F1(-5, 0) and F2(5, 0).
Solution: We have to
2a = 6 → a = 3
F1(-5, 0) and F2(5, 0) → c = 5
From the remarkable relationship, we obtain:
ç² = the² + b^2 → 5² = 3² + b² → b² =25 - 9 → b² = 16 → b = 4
Thus, the reduced equation will be given by:

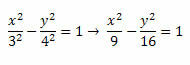
Example 2. Find the reduced hyperbola equation that has two foci with F2 coordinates (0, 10) and imaginary axis measuring 12.
Solution: We have to
F2(0, 10) → c = 10
2b = 12 → b = 6
Using the remarkable relationship, we obtain:
10² = the² + 6² → 100 = a² + 36 → a² = 100 - 36 → a² = 64 → a = 8.
Thus, the reduced hyperbola equation will be given by:

Example 3. Determine the focal length of the hyperbola with equation
Solution: Since the hyperbola equation is of type  We have to
The² = 16 and b² =9
From the remarkable relationship we obtain
ç² = 16 + 9 → c² = 25 → c = 5
The focal length is given by 2c. Thus,
2c = 2*5 =10
So the focal length is 10.

Do not stop now... There's more after the advertising ;)

By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team

Analytical Geometry - Math - Brazil School

Would you like to reference this text in a school or academic work? Look:

RIGONATTO, Marcelo. "Hyperbole"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/hiperbole.htm. Accessed on June 28, 2021.