THE reduced straight equation facilitates the representation of a straight line in the Cartesian plane. At geometry analytical, it is possible to perform this representation and describe the line from the equation y = mx + n, where m is the slope and no is the linear coefficient. To find this equation, it is necessary to know two points on the line, or a point and the angle formed between the line and the x axis in the counterclockwise direction.
Read too: What is straight?
What is the reduced equation of the straight line?
In analytic geometry, we look for a formation law to describe plane figures, such as the circumference, a parable, the line itself, among others. The line has two possibilities of equation, the general equation of the line and the reduced equation of the straight line.
The reduced equation of the line is y = mx + n, on what x and y are, respectively, the independent variable and the dependent variable; m is the slope, and no is the linear coefficient. Furthermore, m and
no are real numbers. With the reduced equation of the line, it is possible to calculate which points belong on this line and which do not.
Angular coefficient
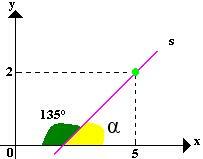
O slope tells us a lot about the behavior of the line, because, from it, it is possible to analyze the slope of the line and identify if it is increasing, decreasing or constant. In addition, the higher the slope value, the higher the angle between the straight line and the x axis, counterclockwise.
To calculate the slope of the line, there are two possibilities. The first is to know that it is the same as tangent from angle α:
m = tgα |
Where α is the angle between the line and the x axis, as shown in the image.
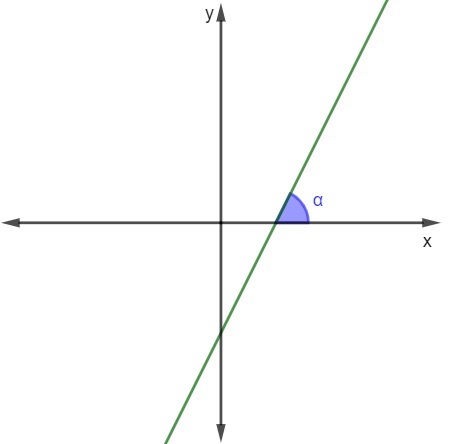
In this case, just know the value of the angle and calculate its tangent to find the slope.
Example:
What is the value of the slope of the following line?
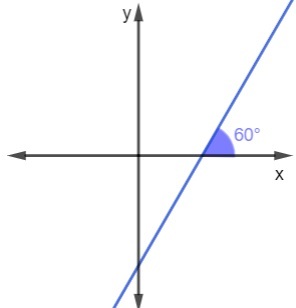
Resolution:
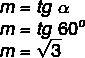
O second method to calculate the slope is knowing two points belonging to the line. Let A(x1yy1) and B (x2yy2), then the slope can be calculated by:
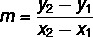
Example:
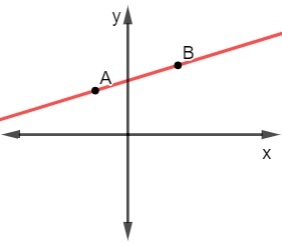
Find the value of the slope of the line represented in the Cartesian plane Next. Consider A(-1, 2) and B(2,3).
Resolution:
As we know two points, we have to:
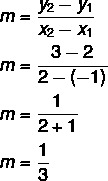
To make the decision on which method to use to calculate the slope of the line, you first need to analyze what the information is that we have. If the value of angle α is known, just calculate the tangent of this angle; now, if we only know the value of two points, then it is necessary to calculate by the second method.
Do not stop now... There's more after the advertising ;)
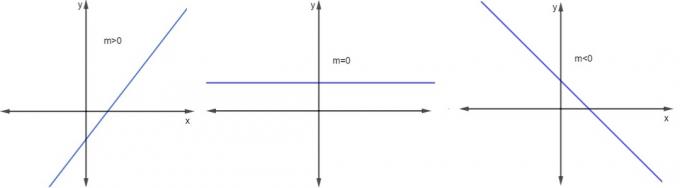
The slope allows us to analyze whether the line is increasing, decreasing or constant. Thus,
m > 0, the line will be increasing;
m = 0 the line will be constant;
m < 0 the line will be decreasing.
Read too: Distance between two points
linear coefficient
O linear coefficient n is the ordinate value when x = 0. This means that n is the y value for the point where the line intersects the y axis. Graphically, to find the value of n, just find the value of y at the point (0,n).

How to Calculate the Reduced Equation of the Line
To find the reduced equation of the line, it is necessary to find the value of m it's from no. By finding the value of the slope and knowing one of its points, it is possible to find the linear coefficient with ease.
Example:
- Find the equation of the line that passes through points A (2,2) and B (3,4).
→ 1st step: find the slope m.
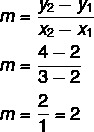
→ 2nd step: find the value of n.
To find the value of n, we need a point (we can choose between point A and B) and the value of the slope.
We know that the reduced equation is y = mx + n. We calculate m = 2 and, using point B(3,4), we will substitute the value of x, y and m.
y = mx + n
4 = 2·3 + n
4 = 6 + n
4 - 6 = n
n = – 2
→ 3rd step: will write equation replacing the value of no and m, which are now known.
y = 2x – 2
This will be the reduced equation of our straight line.
Read too: Intersection point between two straight lines
solved exercises
question 1 - (Enem 2017) In a month, an electronics store starts to make a profit in the first week. The graph represents the profit (L) for that store from the beginning of the month until the 20th. But this behavior extends to the last day, the 30th.
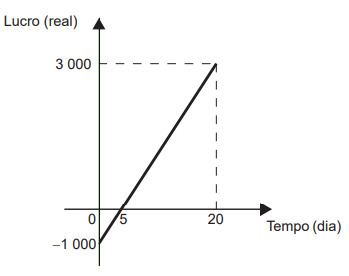
The algebraic representation of profit (L) as a function of time (t) is:
a) L(t) = 20t + 3000
b) L(t) = 20t + 4000
c) L(t) = 200t
d) L(t) = 200t - 1 000
e) L(t) = 200t + 3000
Resolution:
Analyzing the graph, it is possible to see that we already have the linear coefficient n, as it is the point where the line touches the y axis. In this case, n = - 1000.
Now analyzing the points A (0, -1000) and B (20, 3000), we will calculate the value of m.

Hence, L(t) = 200t – 1000.
Letter D
Question 2 - The difference between the value of the linear coefficient and the angular coefficient of the rising line that passes through point (2,2) and makes an angle of 45º with the x axis is:
a) 2
b) 1
c) 0
d) -1
e) -2
Resolution:
→ 1st step: calculate the slope.
Since we know the angle, we know that:
m = tgα
m = tg45º
m = 1
→ 2nd step: find the value of the linear coefficient.
Let m = 1 and A (2.2), performing the substitution in the reduced equation, we have:
y = mx + n
2 = 2 ·1 + n
2= 2 + n
2 - 2 = n
n = 0
→ 3rd step: calculate the difference in the order that was requested, that is, n – m.
0 – 1 = –1
Letter D
By Raul Rodrigues de Oliveira
Maths teacher