The area of a triangle is calculated using the dimensions of the base and height of the triangle using the formula 
, but this formula is only applied to triangles where the height measurement is known. To calculate the area of any triangle we can use other formulas.
Area of a triangle based on the semiperimeter – Heron of Alexandria's Formula
Heron's formula should be used in situations where the value of the three sides of the triangle is known. Given the triangle ABC of sides a, b and c: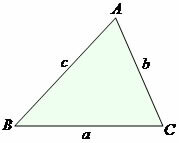
The area of any triangle can be calculated using the following formula:
Where the values of a, b, c correspond to the sides of the triangle and the value of p is the value of the semiperimeter (sum of all sides of a triangle divided by two):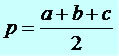
Triangle area using the sine of one of its angles.
Given the triangle ABC of sides a, b, c:
Do not stop now... There's more after the advertising ;)
Observing angle A we can calculate its area through the sine of A, see:
If we take into account the angle C, the area will be calculated using the following formula:
If we take angle B into account, the area will be calculated using the following formula:
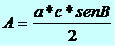
Knowledge of the various ways to calculate the area of a triangle is extremely important in classification assessments, as the student applying such definitions excludes some complex calculations, which may take some time to arrive at a solution. concrete.
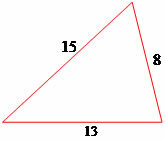
Example 1
Example 2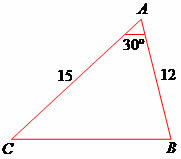
by Mark Noah
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Area of any triangle"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/areas-de-quadrilateros-e-triangulos.htm. Accessed on June 28, 2021.
