The analytical study of the straight line is widely used in everyday problems related to different areas of knowledge, such as physics, biology, chemistry, engineering and even medicine. Determining the straight line equation and understanding its coefficients is very important for understanding of its behavior, being possible to analyze its inclination and the points where it intersects the axes of the flat. On the lines we have the following types of equation: general equation of the line, reduced equation, parametric equation and segmentary equation. We will study the segmentary equation of the straight line and its use.
Consider any line s of the plane of equation ax + by = c. To obtain the segmentary equation of the line s, just divide the entire equation by c, obtaining:
Which is the equation in the segmentary form of the line s.
c/a is the abscissa of the point of intersection with the x axis.
c/b is the y-intercept ordinate
Example 1. Determine the segmentary form of the equation of the line s whose general equation is:
s: 2x + 3y – 6 = 0
Solution: To determine the segmentary equation of the line s we must isolate the independent term c. So, it follows that:
2x + 3y = 6
Dividing the equation by 6, we get: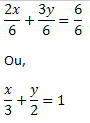
The above identity is the segmentary form of the equation of the line s.
Example 2. Determine the segmentary equation of the line t: 7x + 14y – 28 =0 and the coordinates of the points of intersection of the line with the axes of the plane.
Solution: To determine the segmentary form of the equation of the line t we must isolate the independent term c. Thus, we will have:
7x + 14y = 28
Dividing all equality by 28, we get: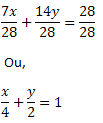
Which is the segmentary equation of the line t.
With the segmentary equation, we can determine the points of intersection of the straight line with the ordered axes of the plane. The term that divides x in the segment equation is the abscissa of the point of intersection of the line with the x axis, and the term that divides y is the abscissa of the point of intersection of the line with the y axis. Thus:
(4, 0) is the point of intersection of the line with the x axis.
(0, 2) is the point of intersection of the line with the y axis.
Do not stop now... There's more after the advertising ;)
by Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
Analytical Geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
RIGONATTO, Marcelo. "Segmental equation of the line"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/equacao-segmentaria-reta.htm. Accessed on July 27, 2021.