Analytical Geometry studies geometric elements in a coordinate system in a plane or space. These geometric objects are determined by their location and position in relation to points and axes of this orientation system.
Since ancient peoples, such as the Egyptians and Romans, the idea of coordinates has already appeared in history. But it was in the 17th century, with the works of René Descartes and Pierre de Fermat, that this field of Mathematics was systematized.
Cartesian orthogonal system
The Orthogonal Cartesian System is a reference base for locating coordinates. It is constituted, in a plane, by two perpendicular axes to each other.
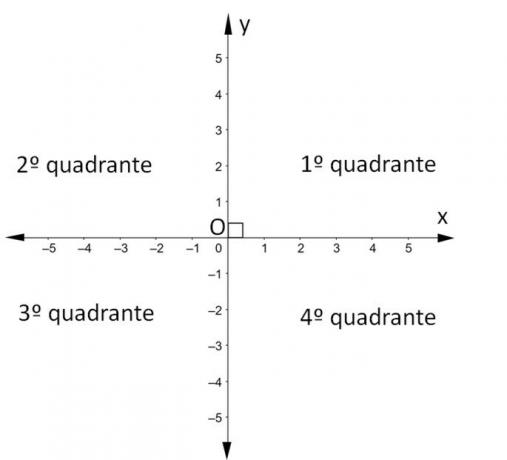
- The O(0,0) origin of this system is the intersection of these axes.
- The x axis is the abscissa.
- The y axis is the ordinate.
- The four quadrants are counterclockwise orientation.
ordered pair
Any point on the plane has the coordinate P(x, y).
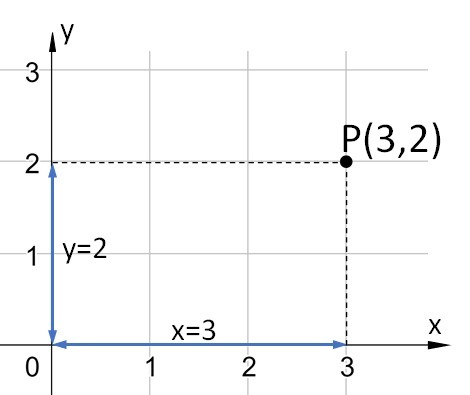
x is the abscissa of point P and constitutes the distance from its orthogonal projection on the x axis to the origin.
y is the ordinate of point P and is the distance from its orthogonal projection on the y axis to the origin.
distance between two points
The distance between two points on the Cartesian plane is the length of the segment joining these two points.
Distance between two points formula and
any.
Midpoint coordinates
Midpoint is the point that divides a segment into two equal parts.
Being the midpoint of a segment
, its coordinates are the arithmetic means of the abscissa and ordinate.
and
Three-point alignment condition
Given the points: .
These three points will be aligned if the determinant of the following matrix is equal to zero.
Example
Angular coefficient of a line
the slope of a straight line is the tangent of its slope
with respect to the x-axis.
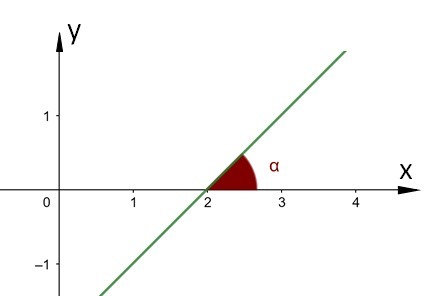
To obtain the slope from two points:
If m > 0, the line is ascending, otherwise, if m < 0, the line is descending.
general equation of the line
Where The,B and ç are constant real numbers and, The and B they are not simultaneously null.
Example
Line equation knowing a point and the slope
given a point and the slope
.
The equation of the line will be:
Example
Reduced form of the straight equation
Where:
m is the slope;
n is the linear coefficient.
no is ordered where the line intersects the y axis.

Example
Look Line Equation.
Relative position between two parallel lines in a plane
Two distinct lines are parallel when their slopes are equal.
if a straight r has slope , and a straight s has slope
, these are parallel when:
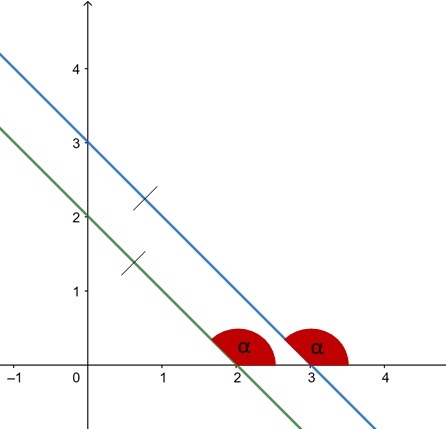
For this, your inclinations must be equal.
Tangents are equal when angles are equal.
Relative position between two competing straight lines in a plane
Two lines are concurrent when their slopes are different.
In turn, the slopes differ when their angles of inclination with respect to the x axis are different.
perpendicular lines
Two remainders are perpendicular when the product of their slopes is equal to -1.
two straights r and s, distinct, with slopes and
, are perpendicular if, and only if:
or
Another way to know if two lines are perpendicular is from their equations in general form.
The equations of the lines r and s being:
Two lines perpendicular to it when:
Look Perpendicular Lines.
Circumference
Circumference is the locus on the plane where all points P(x, y) are the same distance r from its center C(a, b), where r is the measure of being radius.
Circumference equation in reduced form
Where:
r is the radius, the distance between any point on your arc and the center. Ç.
The and B are the coordinates of the center Ç.
general equation of the circle
It is obtained by developing the squared terms of the reduced equation of the circumference.
It is very common to show the general form of the circumference equation in exercises, also known as the normal form.
conical
The word conic comes from a cone and refers to the curves obtained by sectioning it. Ellipse, hyperbola and parabola are curves called conic.
Ellipse
Ellipse is a closed curve obtained by sectioning a straight circular cone by a plane oblique to the axis, which does not pass through the vertex and is not parallel to its generatrices.
In a plane, the set of all points whose sum of distances to two internal fixed points is constant.
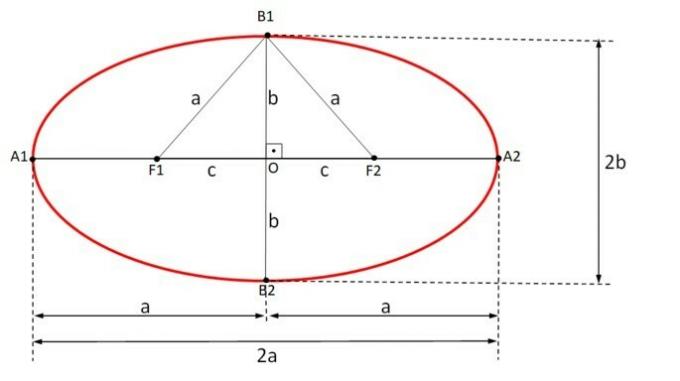
Ellipse elements:
- F1 and F2 are the foci of the ellipse;
- 2c is the focal length of the ellipse. It is the distance between F1 and F2;
- The point O it's center of the ellipse. It is the midpoint between F1 and F2;
- A1 and A2 are the vertices of the ellipse;
- the segment
major axis and equal to 2a.
- the segment
minor axis is equal to 2b.
- Eccentricity
where 0 < and < 1.
Reduced Ellipse Equation
Consider a point P(x, y) contained in the ellipse where x is the abscissa and y is the ordinate of this point.
Center of the ellipse at the origin of the coordinate system and major axis (AA) on the x-axis.

Center of the ellipse at the origin of the coordinate system and major axis (AA) on the y axis.
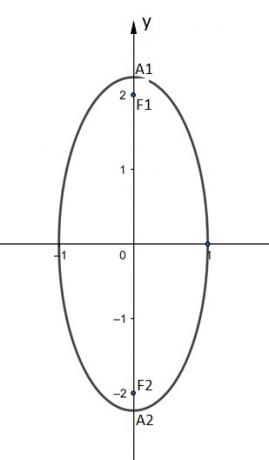
Reduced equation of the ellipse with axes parallel to the coordinate axes
considering a point as the origin of the Cartesian system and, a point
as the center of the ellipse.
AA major axis, parallel to the x axis.
AA major axis, parallel to the y axis.
Hyperbole
Hyperbola is a set of points on a plane where the difference between two fixed points F1 and F2 results in a constant, positive value.

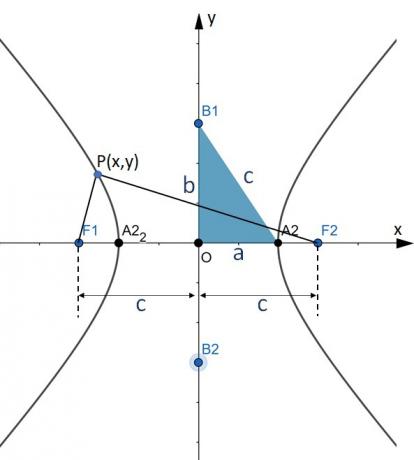
Elements of hyperbole:
- F1 and F2 are the foci of hyperbola.
- 2c =
is the focal length.
- Center of hyperbole is the point O, F1F2 segment average.
- A1 and A2 are the vertices.
- 2a = A1A2 is the real or transverse axis.
- 2b = B1B2 is the imaginary or conjugate axis.
-
is the eccentricity.
Through triangle B1OA2
Hyperbola reduced equation
With real axis about x axis and center at origin.
With real axis on y axis and center at origin.
Hyperbola equation with axes parallel to coordinate axes
AA real axis parallel to x axis and center .
Real axis AA parallel to y axis and center .
Parable
Parabola is the locus where the set of points P(x, y) are the same distance from a fixed point F and a line d.
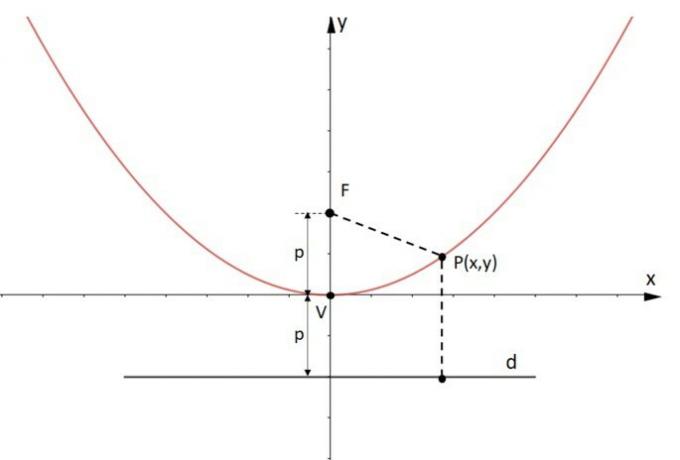
Elements of the parable:
- F is the focus of the parable;
- d is the straight guideline;
- Symmetry axis is the straight line through focus F and perpendicular to the guideline.
- V is the vertex of the parabola.
- p is the segment of the same length between focus F and vertex V e, between vertex and directive d.
Reduced equations of the parabola
With vertex at the origin and symmetry axis on the y axis.
If p>0 concavity upwards.
If p<0 downward concavity.
With vertex at the origin and symmetry axis on the x axis.
If p>0 concavity to the right.
If p<0 concavity to the left.
With symmetry axis parallel to y axis and vertex .
With symmetry axis parallel to the x axis and vertex .
practice with Exercises on Analytical Geometry.
Learn more at:
Cartesian Plan
distance between two points
conical
Calculation of Angular Coefficient