THE lawinhook states that when a spring is deformed by some strength external, a strengthelastic restorative starts to be exercised in the samedirection and in the senseopposite to external force. This elastic force, in turn, is variable and depends on the size of the deformation that is suffered by the spring.
Lookalso:Physics formula tricks
Hooke's law and elastic force
According to the Hooke's law, when a force is applied on a spring, it is able to deform the spring, consequently, the spring produces a force opposite to the external force, called strengthelastic. This strength becomes greater according to the deformation of spring. see the formula used to calculate the strengthelastic:
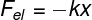
Fhe – tensile strength (N)
k - elastic constant (N/m)
x - spring deformation (m)
In the formula above, it is possible to observe the presence of a signalnegative. This sign concerns the sense of the elastic force, which is always opposite to the variation in length suffered by the spring (x). If this variation is positive, the force is negative, that is, has senseopposite.

Hooke's Law Graph
Based on the formula above, we can build a graph that relates the elastic force to the modulus of the spring's deformation. When doing so, the graphic will have the following profile:

Analyzing the graph above, it is possible to notice that when a force of 40 N is applied to the spring, its deformation is 0.5 m. In addition, the spring force also has a modulus of 40 N, according to Newton's third law, the law of action and reaction. Let's calculate the constantelastic of this spring in question based on the module of the strengthelastic.

The calculation indicates that the constantelastic this spring is 80 N/m, but what does that mean? Next, we bring a brief topic dedicated to the elastic constant and its meaning.
Spring elastic constant
THE constantelastic measures the stiffness of the spring, that is, the force that is needed to make the spring suffer a deformation. Springs that have large elastic constants are more difficult to deform, that is, to make their length vary, it is necessary to apply a greater force. The elastic constant is a scalar greatness, and its unit of measure, according to the International System of Units, is the N/m (newton per meter).
imagine that a spring it has an elastic constant of 800 N/m. This spring will need to be compressed or stretched by a force of at least 800 N for its length to change by 1 m. Thus, if we wanted this spring to have its length varied by 0.5 m, the minimum force required to do so would be 400 N.
Read too: Five Tips for Solving Physics Exercises
Spring deformation or elongation
THE deformation or elongation is the measure of the variation in the length of the spring. In this sense, it can be calculated by difference between the lengthFinal it's the lengthinitial of spring. When the spring is in its original size, free from the action of forces that deform it, there is no elongation.
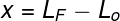
x - spring deformation (m)
LF – final spring length (m)
L0 – initial spring length (m)
Note that, in the formula above, if the final length of the spring (LF) is greater than the initial length (L0), the deformation will be positive (x > 0); otherwise, when the final length of the spring is less than the initial length, the deformation will be negative (x<0).
See too:Seven Most Common Mistakes Made in the Study of Physics
Solved exercises on Hooke's law
Question 1) A spring with an elastic constant equal to 200 N/m has a length of 20 cm. When subjected to an external force, the length of this spring becomes 15 cm. Determine the magnitude of the elastic force exerted by the spring when compressed by 15 cm.
a) 40 N/m
b) 10 N/m
c) 30 N/m
d) 15 N/m
e) 25 N/m
Template: letter B.
Spring deformation is measured by the difference between its original length and its size when subjected to an external force. In this case, the spring elongation is 5 cm or 0.05 m. Based on this, let's do the calculations:
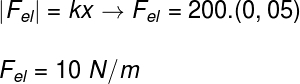
Question 2) When compressed by a force of 4 N, a spring changes its length by 1.6 cm (0.016 m). The elastic constant of this spring, in N/m, is about:
a) 6.4 N/m
b) 500 N/m
c) 250 N/m
d) 256 N/m
e) 12.8 N/m
Template: letter C.
Let's do the calculation according to Hooke's law:
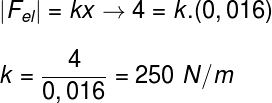
Question 3) Regarding the elastic force, described mathematically by Hooke's law, mark the alternative CORRECT:
a) The greater the elastic constant of a spring, the less force it takes to deform it.
b) Elastic force is inversely proportional to spring elongation.
c) The force that is exerted on the spring, deforming it, is equal to the elastic force generated by the spring.
d) The elastic force has its maximum value when the spring is in its original shape.
e) The spring constant is a scalar quantity, measured in newtons per gram.
Template: letter B.
Let's look at the alternatives:
The) fake: How much smaller is the elastic constant of a spring, the less force it takes to deform it.
B) fake: Elastic strength is directly proportional to the elongation of the spring.
c) True.
d) fake: Elastic strength has its value Minimum when the spring is in its original shape.
and) fake: The elastic constant of the spring is a scalar quantity, measured in newtons per subway.
By Rafael Hellerbrock
Physics teacher

