Radical multiplications and divisions must occur when the root indices are equal. In this occurrence, we must repeat the radical and multiply the radicands. Let's remember the elements of a radical:
n: index
x: rooting
y: exponent of the radicand
Let's go through examples, determine the practical way to reduce to the same index.
Example 1
Let's multiply the index of the 1st radical by the value of the index of the 2nd radical and vice versa, introducing the multiplier term as an exponent of the radicand. Watch:

Example 2
Do not stop now... There's more after the advertising ;)
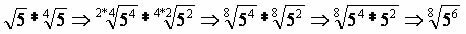
Example 3 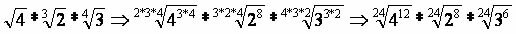
Example 4
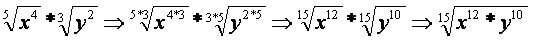
These techniques are used in situations in which the calculations shown are represented by elements linked to radicals. For example, 2nd degree equations have a part involving roots, so at some point we must use such techniques to obtain the result.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Numerical sets - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Reduction of Radicals to the Same Index"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/reducao-radicais-ao-mesmo-Indice.htm. Accessed on June 28, 2021.