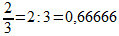A number can be characterized as odd or even. To make this differentiation, we need to know some definitions:
Even number is any number that, divided by two, generates as a remainder the number zero. a number is considered odd when, by dividing it by two, it results in a nonzero remainder. Example:
Check the set number {23, 42} which is even and which is odd.
23| 2
-2 11
03
-02
01
23 is an odd number because its remainder is non-zero.
42 | 2
-4 21
02
-02
00
42 is an even number since its remainder is zero.
We just remembered the definition for even and odd number. Before talking about the properties themselves, it is necessary to remember that the grouping of even and odd numbers is given by a formation law. the grouping of pair numbers respects training law 2.n, and the grouping of odd numbers has as a law of formation 2.n + 1. Understand as "n" any number of the set of integers. See the training law application for odd and even numbers in the following example.
Example: Find the first five odd and even numbers using their respective formation laws.
Even numbers → Formation law: 2.n
First six numeric terms: 0, 1, 2, 3, 4, 5
2.n = 2. 0 = 0
2.n = 2. 2 = 2
2.n = 2. 2 = 4
2.n = 2. 3 = 6
2.n = 2. 4 = 8
2.n = 2. 5 = 10
The first five even numbers are: 2, 4, 6, 8, 10
Odd numbers → Formation law: 2.n + 1
First five numeric terms: 1, 2, 3, 4, 5
2.n + 1 = 2. 0 + 1 = 1
2.n + 1 = 2. 1 + 1 = 3
2.n + 1 = 2. 2 + 1 = 5
2.n + 1 = 2. 3 + 1 = 7
2.n + 1 = 2. 4 + 1 = 9
2.n + 1 = 2. 5 + 1 = 11
Now let's learn the five properties of odd and even numbers:
Do not stop now... There's more after the advertising ;)
First property:The sum of two even numbers always forms an even number.
Examples: Check that the sum of the even numbers 12 and 36 makes an even number.
36
+12
48
To check if 48 is an even number, we must divide it by two.
48 | 2
-48 24
00
Since the remainder of the division of 48 by two is zero, then 48 is even. With that, we check the validity of the first property.
Second property: By adding two odd numbers, we will get an even number.
Example: Add the numbers 13 and 17 together and check if it gives an odd number.
13
+17
30
Let's check if 20 is even.
30 | 2
-30 15
00
The remainder of the 20-by-2 division is zero; therefore, 20 is an even number. Therefore, the second property is valid.
Third property: When we multiply two odd numbers, we get an odd number as a result.
Example: Check that the product of 7x5 and 13x9 results in odd numbers.
7 x 5 = 35
35 | 2
-34 17
01
The number 35 is odd.
13 x 9 = 117
117 | 2
-116 58
001
The number 177 is odd.
So, when we multiply two odd numbers, we get a number that is also odd. Thus, the validity of the third property is proven.
Fourth property:When we multiply any number by an even number, we will always get an even number.
Example: Make the product of 33 by 2 and check that the result is an even number.
33 x 4 = 132
132 | 2
-132 66
000
From the product of 33 by 4, we got the answer number 132, which is even, so the fourth property is valid.
Fifth property: By multiplying two even numbers, we get an even number as a result.
Example: Multiply 6 by 4 and check if the product is an even number.
6 x 4 = 24
24 | 2
-24 12
00
The number 24, taken from the product of 6 by 4, is even. With that, we prove the validity of the fifth property.
By Naysa Oliveira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Naysa Crystine Nogueira. "Even and odd number properties"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/propriedades-dos-numeros-pares-impares.htm. Accessed on June 28, 2021.