Mathematics is present in many everyday situations, but sometimes people cannot associate the fundamentals proposed by the textbook, through the teacher, with such situations. MMC (Least Common Multiple) and MDC (Maximum Common Divisor) have numerous everyday applications. Let's remember how to calculate MMC and MDC between numbers, note:
Minimum common multiple between 12 and 28
The numbers are factored at the same time, that is, divided by the same number. The split quotient is placed below the dividend. This process must take place until the total simplification of the dividend.
MMC (12, 28) = 2 × 2 × 3 × 7 = 84
The least common multiple between the numbers 12 and 28 is 84.
Maximum common divisor between 75 and 125
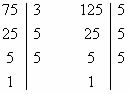
75 = 3 * 5 * 5
125 = 5 * 5 * 5
Note that the multiplication of the coincident prime factors in the two factorizations forms the greatest common divisor, so:
The MDC between (75, 125) = 5 * 5 = 25
Let's introduce some everyday applications involving MMC and MDC.
Example 1
A fabric industry manufactures patches of the same length. After making the necessary cuts, it was found that two remaining pieces had the following measurements: 156 centimeters and 234 centimeters. When the production manager was informed of the measurements, he ordered the employee to cut the cloth in equal parts and as long as possible. How can he resolve this situation?
We should find the MDC between 156 and 234, this value will correspond to the desired length measurement.

Prime factor decomposition
234 = 2 * 3 * 3 * 13
156 = 2 * 2 * 3 * 13
MDC (156, 234) = 2 * 3 * 13 = 78
Therefore, the flaps can be 78 cm long.
Example 2
A logistics company is made up of three areas: administrative, operational and salespeople. The administrative area is made up of 30 employees, the operational area has 48 and the sales area has 36 people. At the end of the year, the company integrates the three areas, so that all employees actively participate. Teams should contain the same number of employees with as many as possible. Determine how many employees should be on each team and as many teams as possible.
Find the MDC between numbers 48, 36 and 30.
Do not stop now... There's more after the advertising ;)
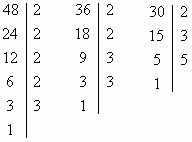
Prime factor decomposition
48 = 2 * 2 * 2 * 2 * 3
36 = 2 * 2 * 3 * 3
30 = 2 * 3 * 5
MDC (30, 36, 48) = 2 * 3 = 6
Determining the total number of teams:
48 + 36 + 30 = 114 → 114: 6 = 19 teams
The number of teams will be equal to 19, with 6 participants each.
Example 3
(PUC–SP) On a production line, a certain type of maintenance is performed on machine A every 3 days, machine B every 4 days, and machine C every 6 days. If on December 2 the maintenance was carried out on the three machines, after how many days the machines will receive maintenance on the same day.
We have to determine the MMC between the numbers 3, 4 and 6.
MMC (3, 4, 6) = 2 * 2 * 3 = 12
We conclude that after 12 days, maintenance will be done on all three machines. So, December 14th.
Example 4
A doctor, when prescribing a prescription, determines that three medications are taken by the patient according to the following schedule: remedy A every 2 hours, remedy B every 3 hours and remedy C every 6 hours. If the patient uses the three medicines at 8 am, what will be the next time to take them?
Calculate the MMC of numbers 2, 3 and 6.

MMC(2, 3, 6) = 2 * 3 = 6
The least common multiple of the numbers 2, 3, 6 is equal to 6.
Every 6 hours the three medicines will be taken together. Therefore, the next time will be at 2 pm.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Numerical Set- Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "MMC and MDC Applications"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/aplicacoes-mmc-mdc.htm. Accessed on June 28, 2021.