We can say that a angle is the region of the plane limited by two semi-straight of the same origin. Watch:
complementary angles
anglescomplementary they are two angles whose sum results in 90º, that is, one is the complement of the other.
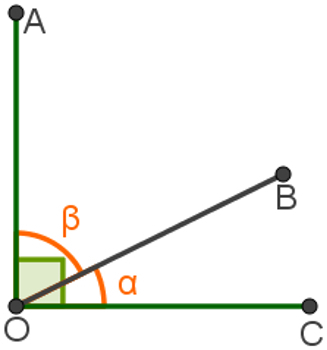
Angles whose sum equals 90°
In the illustration, we have to:
α + β = 90º
α = 90º – β
β = 90º – α
supplementary angles
anglessupplementary they are two angles that, added together, are equal to 180º, thus, one is the supplement of the other.

Angles whose sum equals 180°
In the illustration, we have to:
α + β = 180º
α = 180º – β
β = 180º – α
adjacent angles
Do not stop now... There's more after the advertising ;)
anglesadjacent are those that have one side in common, but the given regions have no common points. Note the illustration:

Angles that have sides in common
Angles AÔB and BÔC are adjacent, as they have the OB side in common, but their determined regions do not have points in common.
Angles AÔC and AÔB are not adjacent, although they have one side in common, as their particular regions have points in common. Region AÔB belongs to region AÔC.
Adjacent and supplementary angles
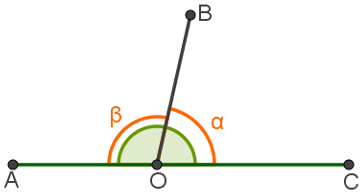
According to the illustration above, angles AÔB and BÔC are adjacent, as they have the OB side in common and their determined areas do not have double points. They are also supplementary, since the sum of angles α and β totals 180º.
by Mark Noah
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Complementary, supplementary and adjacent angles"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/angulos-complementares-angulos-suplementares-angulos-.htm. Accessed on June 28, 2021.



