Addition is the act of joining elements, one of the four basic operations of arithmetic. Addition is linked to the idea of adding. Every time we join new elements or values, we are adding.
In Mathematics, the symbol + is used to represent an addition.
terms of addition
Each summed element is called a parcel. An addition can have at least two and even infinite installments.
Example
By joining 300 grams of rice with 200 grams of beans, we have a dish with 500 grams.
The installments are 300 and 200 and the result is called total or sum. In the example, the result 500 is the total or the sum.

Addition account: calculation of addition
Also known as count of plus or, count of addition, is a procedure that helps us to calculate. This addition algorithm is very useful, especially for additions with many parts or large values.
When making an addition, the plots are written on top of each other, as a “stack” of plots and a line is drawn below.
We perform the addition by adding the digits with the same order, starting with the units. Then we continue adding the numbers, order by order.
Example
23 + 15 = 38
When writing the numbers, they must be organized by placing equal orders in the same column. Units over units, tens over tens, and so on.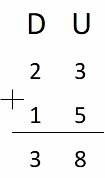
Addition with reservation or regrouping
Addition with reservation or regrouping is also known as: "go one", "go two".... When adding the digits in an order, if the result is greater than 9, we must add this quantity to the next order.
Remember that we cannot write more than one digit in order.
Example
459 + 232 =
In order of units we have 9 + 2 = 11. The number 11 can be written as 1 ten + 1 unit:
11 = 10 + 1
This ten must be added to the tens column.

In the tens column we have +1 ten which will be added to 5 and 3. As 1 + 5 + 3 = 9, it is not necessary to add a hundred and so, we follow the calculation.
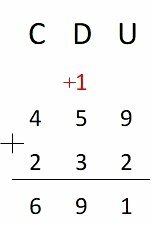
This procedure must be repeated in any order if the sum is greater than 9. When completing a next order, we must always add it in the correct column.
Addition properties
The addition operation with natural numbers has five properties, and in the set of integers there is one. These properties define addition and help to calculate.
Associative Property
We can associate the installments in order to facilitate the calculation.
Example
8 + 6 + 2 + 3= 19
We can associate the parcels as follows:
8 + 2 + 6 + 3 = 19
10 + 9 = 19
Commutative Property
The order of the installments does not change the sum.
12 + 3 = 15, as well as 3 + 12 = 15.
neutral element
The neutral element of addition is zero, as it does not change the result.
Examples
5 + 0 = 5
4 + 0 + 5 = 9
0 + 37 = 37
Closure
The closing property defines that when adding two or more natural numbers, the result will always be a natural number.
Example
1 457 + 2 354 = 3 811
Remember that the set of natural numbers starts with zero and goes to infinity, advancing by one unit.
N = {0,1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …}
Opposite or symmetrical element property
In the set of integers there is the property of the opposite or symmetrical element, in which a number is opposite or symmetrical when its sign is changed. Ex.: The opposite or symmetrical of 2 is -2.
When adding symmetric numbers, the result is always zero.
Examples
3 + (-3) = 0
-17 + 17 = 0
256 + (-256) = 0
See too addition properties.
Rule of signs in addition (addition of whole numbers)
The set of integers comprises the negative and positive numbers. Also, the set of integers is infinite, both in the negative and positive directions of the line.
Z = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, …}
To add whole numbers, some sign rules are respected.
equal signs
If the parcels have the same sign, the sign must be added and repeated.
Examples
7 + 2 = 9
-14 - 3 = -17
different signs
If the parcels have different signs, you must subtract and keep the sign of the number with the highest absolute value.
- 21 + 12 = 21 - 12 = -9 (because the minus sign is at 21)
15 - 17 = 17 - 15 = -2 (because the minus sign is at 17)
addition exercise
Solve the following additions using the addition algorithm.
a) 561 + 1364 =
b) 2642 + 3471 =
The) 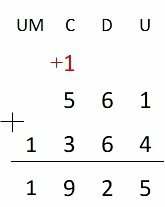
B) 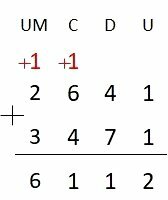
Look subtraction and division.
Fun fact: the + and - symbols
The symbols of addition +, and subtraction -, appear for the first time in history in 1498, recorded in the book Commercial Arithmetic, by the German Johannes Widmann. Although they were used to represent excesses and deficits of goods.
In 1557 the Englishman Robert Recorde in his work, Whetstone of Witte, used these symbols with the usual sense of adding and subtracting.

