The domain, range and range are numerical sets related by mathematical functions. These transform values through their formation laws and transport them from an output set, the domain, to an arrival set, the range.
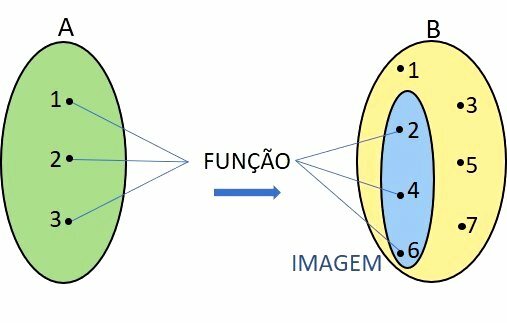
From the domain set come the values that will be transformed by the function formula, or formation law. Afterwards, these values arrive at the codomain.
The subset formed by the elements that arrive in the codomain is called the image set.
In this way, domain, range and range are non-empty sets and can be finite or infinite.

In the study of functions, it is necessary to specify which elements or the scope of these sets. For example: set of natural numbers or set of real numbers.
Given a domain A in which each element x that belongs to it is transformed by the function into an element y that belongs to the range B, each element y is called an image of x.
To designate the domain and range of a function, the notation is used:
(we read f from A to B)
These transformation laws are expressions that involve operations and numerical values.
Example
A function f: A→B defined by the formation law f(x) = 2x, where its domain is the set A={1, 2, 3} and the range B={1, 2, 3, 4, 5, 6, 7}, can be represented by the values in the table and the diagrams:
|
Domain x |
f(x) = 2x |
Image and |
|---|---|---|
| 1 | f(1) = 2. 1 | 2 |
| 2 | f(2) = 2. 2 | 4 |
| 3 | f(3) = 2. 3 | 6 |
Organizing table results into diagrams:
Domain
Domain D of a function f is the output set, composed of the elements x applied to the function.
Geometrically, in a Cartesian plane, the domain elements form the x-axis of the abscissa.
in the notation the domain is represented by the letter before the arrow.
Every element x in the domain has at least one image y in the codomain.
codomain
CD domain is the arrival set. in the notation is represented on the right side of the arrow.
Image
Image Im is a subset of the range, formed by the elements y that leave the function and arrive at the range, which may have the same number of elements, or a smaller number.
In this way the image set of a function f is contained in the codomain.
Geometrically, in a Cartesian plane the elements of the image set form the y-axis of the ordinates.
It is common to say that y is the value assumed by the function f(x) and, in this way, we write:
It is possible that the same element y is an image of more than one element x in the domain.
Example
in function defined by law
, for symmetric x-values of the domain, we have a single y-image.
learn more about functions.
Domain, co-domain and image exercises
Exercise 1
Given the sets A = {8, 12, 13, 20, 23} and B = {10, 17, 22, 24, 25, 27, 41, 46, 47, 55}, determine: domain, range and range of the functions.
a) f: A → B defined by f (x) = 2x + 1
b) f: A → B defined by f (x) = 3x - 14
a) f: A → B defined by f (x) = 2x + 1
Domain A = {8, 12, 13, 20, 23}
Domain B = {10, 17, 22, 24, 25, 27, 41, 46, 47, 55}
Image Im (f) ={17,25,27,41,47}
| D(f) | f(x)=2x+1 | Im (f) |
|---|---|---|
| 8 | f (8)=2.8+1 | 17 |
| 12 | f (12)=2.12+1 | 25 |
| 13 | f (13)=2.13+1 | 27 |
| 20 | f(20)=2.20+1 | 41 |
| 23 | f (23)=2.23+1 | 47 |
b) f: A → B defined by f (x) = 3x - 14
Domain A = {8, 12, 13, 20, 23}
Domain B = {10, 17, 22, 24, 25, 27, 41, 46, 47, 55}
Image Im (f) ={}
| D(f) | f(x) = 3x - 14 | Im (f) |
|---|---|---|
8 |
f (8)=3.8 - 14 | 10 |
| 12 | f (12)=3.12 - 14 | 24 |
| 13 | f (13)=3.13 - 14 | 25 |
| 20 | f (20)=3.20 - 14 | 46 |
| 23 | f (23)=3.23 - 14 | 55 |
Exercise 2
Determine the domain of functions defined by:
The domain is the set of possible values that x can take.
a) We know that it is not possible to have division by zero 0, so the denominator must be different from zero.
We read: x belongs to the reals such that x is different from 2.
b) There is no square root of a negative number. Therefore, the radicand must be greater than or equal to zero.
We read: x belongs to the reals such that x is greater than or equal to 5.
Exercise 3
Given the function with domain in the set of integers what is the image set of f(x) ?
The set Z of integers admits negative and positive numbers where two consecutive numbers are 1 unit apart.
In this way, the function admits positive and negative values. However, since x is squared, every value, even a negative one, will return a positive value.
Example
f(-2) = (-2)² = -2. (-2) = 4
This way, there will only be natural numbers in the image.
You may be interested in:
- injection function
- Surjective Function
- Bijection Function
- Inverse Function
- Composite Function
Applications and curiosities
Functions have application in the study of any phenomenon in which one parameter depends on another. As, for example, the speed of a piece of furniture over time, the effects of a drug with the characteristics of acidity in the stomach, the temperature of a boiler with the amount of fuel.
The functions are present in real phenomena and, therefore, have application in all scientific and engineering studies.
The study of functions is not recent, some records in Antiquity in Babylonian tables show that they were already part of mathematics. Over the years, the notation, the way they are written, has been receiving contributions from several mathematicians and improving, until we use them today.