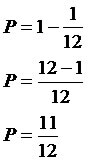Study arithmetic and geometric progression with solved and commented exercises step by step.
Exercise 1
In an AP, a2 = 5 and a7 = 15. Find a4 and add the first five terms of this AP.
Correct answer: a4 = 9 and S = 35.
Resolution
1st step: determine the reason and a4.
To leave a2 and arrive at a7, we add 5r, as it is the "distance" between 7 and 2.
The term a4 is the term a2 plus 2r, because to get from a2 to a4, we "advance" 2r. Soon,
Therefore, the fourth term of AP is 9.
2nd step: determine the sum of the first five terms of this AP.
The sum of the terms of an AP is given by:
a1 = a2 - r (because we go back one position in PA, starting from a2)
a1 = 5 - 2 = 3
a5 = a7 - 2r (because we go back two positions in PA, starting from a7).
a5 = 15 - 2.2 = 15 - 4 = 11
Exercise 2
(Aeronautics 2021) A professor wrote an 8-term increasing arithmetic progression starting with the number 3 and made up of only natural numbers. He then noticed that the second, fourth and eighth terms of this arithmetic progression formed, in that order, a geometric progression. The professor also observed that the sum of the terms of this geometric progression was equal to
a) 42
b) 36
c) 18
d) 9
Answer: a) 42
By AP, the terms that form a PG are a2, a4 and a8:
The sum of the three terms is:
To determine r, we use the geometric mean:
Squareing both sides
Squaring the first term and distributing the second term:
Substituting r into equation I, we have:
Therefore, the sum of the first three terms is equal to 42.
Exercise 3
(PM-SP 2019) In 2015, a large oil company started the process of reusing the water used to cool the parts that produced and made a projection of a gradual increase, in arithmetic progression, until the year 2050, of the volume of water that will be reused, year by year year.
The table shows the volumes of water reused in the first 3 years:

Let An be the general term of the arithmetic progression that indicates the volume of reused water, in millions of m³, with n = 1, representing the volume of water reused in the year 2016, n = 2, representing the volume of water reused in the year 2017, and so on successively.
Under these conditions, one has to
a) An = 0.5n – 23.5.
b) An = 23.5 + 0.5n.
c) An = 0.5n + 23.
d) An = 23 – 0.5n.
e) An = 0.5n - 23.
Correct answer: c) An = 0.5n + 23.
objective
Determine An as a function of n.
Resolution
The ratio of the arithmetic progression is 0.5, because 24 - 23.5 = 0.5.
a1 = 23.5
The general term of an AP is given by:
Substituting the values:
Exercise 4
(CEDERJ 2021) The sequence (2x+3, 3x+4, 4x+5, ...) is an arithmetic progression of ratio 6. The fourth term of this progression is
a) 31.
b) 33.
c) 35.
d) 37.
Correct answer: a) 31
Resolution
The fourth term is a3 + r, like this:
Substituting the found values:
Exercise 5
(Enem 2021) In Brazil, the time required for a student to complete his training until graduation in a higher course, considering 9 years of elementary school, 3 years of high school and 4 years of graduation (average time), it is 16 years old. However, the reality of Brazilians shows that the average time of study of people over 14 years old is still very small, as shown in the table.
Consider that the increase in study time, at each period, for these people, remains constant until the year 2050, and that it is intended to reach the level of 70% of the time required to obtain the higher education given previously.
The year in which the average time of study of people over 14 years old will reach the desired percentage will be
a) 2018.
b) 2023.
c) 2031.
d) 2035.
e) 2043.
Correct answer: d) 2035.
1st part: determine 70% of 16.
2nd part: determine after how many periods will 11.2 years of study be reached.
The study time sequence is an arithmetic progression (AP) with a ratio of 0.6.
r = a2 - a1 = 5.8 - 5.2 = 0.6
a1 = 5.2
The amount 11.2 years will be reached in:
The amount of 11.2 will be reached in the 11th term of the PA.
3rd part: determine which is the 11th term of the PA of the years.
The ratio is a2 - a1 = 1999 - 1995 = 4 years
Conclusion
70% of the 16 years required to complete an undergraduate degree will be reached in 2035.
Exercise 6
(Fire Department 2021) An airplane and a fire truck have water reservoirs with capacities of 12,000 and 8,000 liters of water, respectively. The truck has a 2.5 GPM pump, meaning it is capable of pumping 2.5 gallons per minute.
From this hypothetical situation, judge the following item, considering that 1 gallon is equal to 3.8 liters of water.
If a water tank has a capacity of X thousand liters, so that 8, X and 12 are in geometric progression, in that order, then the capacity of that tank is less than 10 thousand liters.
Right
Wrong
Correct answer: right
objective
Check if X < 10.
Resolution
In a geometric progression, PG, the middle term is the geometric mean between the extremes.
In fact, the approximate square root of 96 is 9.79. We conclude that the capacity X of the tank is less than 10 thousand liters.
Exercise 7
(Aeronautics 2021) Be the P.G. (24, 36, 54, ...). By adding the 5th and 6th terms of this G.P. there has been
a) 81/2
b) 405/2
c) 1215/4
d) 1435/4
Correct answer: c) 1215/4
objective
Add a5 + a6
Resolution
Step 1: Determine the ratio q.
The reason for PG is:
Step 2: Determine a5
a4 = a3. q
a5 = a4. q
Substituting a4 into a5:
Step 3: Determine a6
a6 = a5. q
Substituting a5 into a6:
Step 4: Add a5 + a6 replacing the numeric values.
Putting 54 in evidence:
Exercise 8
(UERJ 2019) The triangles A1B1C1, A2B2C2, A3B3C3, illustrated below, have perimeters p1, p2, p3, respectively. The vertices of these triangles, starting from the second, are the midpoints of the sides of the previous triangle.
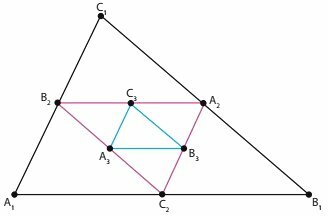
admit that .
Thus, (p1, p2, p3) defines the following progression:
a) ratio arithmetic = – 8
b) ratio arithmetic = – 6
c) geometric ratio = 1/2
d) geometric ratio = 1/4
Correct answer: c) geometric ratio = 1/2
Resolution
Step 1: define the perimeters p1, p2 and p3.
By parallelism, we verify that the sides of the interior triangle are half of the immediately exterior one.
For example, B2A2 = A1C2
Thus, p2 is half of p1, just as p3 is half of p2. We have:
Step 2: Assemble the progression and classify it.
It turns out that to determine p2, 18 is multiplied by 1/2.
Also, 9 multiplied by 1/2 is 4.5.
Conclusion
We verify that the progression is geometric, with a ratio of 1/2.
Exercise 9
(Enem 2021) The graph informs the production registered by an industry in the months of January, March and April.
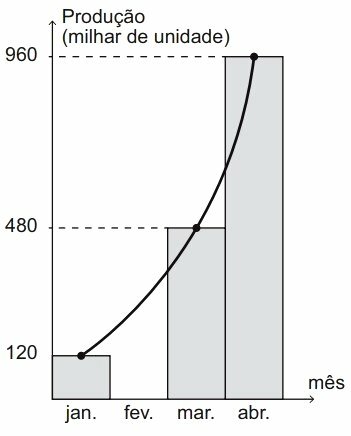
Due to logistical problems, the production survey for the month of February was not carried out. However, information for the other three months suggests that production in this four-month period grew exponentially, as shown by the trend curve drawn in the graph.
Assuming that the growth in this period was exponential, it can be inferred that the production of this industry in the month of February, in thousands of units, was
a) 0.
b) 120.
c) 240.
d) 300.
e) 400.
Correct answer: c) 240.
Resolution
The general term of a PG is an exponential a as a function of n, where a1 and q are constant numbers.
a1 = 120
The ratio q, can be determined by a4 / a3, like this:
The February quantity is a2, which is obtained by multiplying a1 by q.
Therefore, the production in the month of February was 240.
Study more with:
- Geometric progression exercises
- Arithmetic progression exercises
See too:
- PA and PG: summary, formulas and exercises
- Geometric progression
- arithmetic progression