THE arithmetic progression (AP) is numerical sequence that we use to describe the behavior of certain phenomena in mathematics. In a PA, the growth or decay is always constant, that is, from one term to another, the difference will always be the same, and this difference is known as reason.
As a result of the predictable behavior of a progression, you can describe it from a formula known as general term. For this same reason, it is also possible to calculate the sum of the terms of a PA using a specific formula.
Read too: Geometric progression - how to calculate?
What is a PA?
Understanding that a PA is a sequence of terms in which the difference between a term and its previous one is always constant, to describe this progression from a formula, we need to find the initial term, or that is, the first term of a progression, and its reason, which is this constant difference between the terms.
Generally speaking, the PA is written as follows:
(The1, a2,The3, a4,The5, a6,The7, a8)
The first term is the a1 and, from it, to the add the reason r, let's find the successor terms.
The1 + r = a2
The2 + r = a3
The3 + r = a4
...
So, to write the arithmetic progression, we need to know who is its first term and why.
Example:
Let's write the first six terms of an AP knowing that its first term is 4 and its ratio equals 2. knowing the1 =4 and r = 2, we conclude that this progression starts at 4 and increases from 2 to 2. Therefore, we can describe its terms.
The1 = 4
The2 = 4+ 2 = 6
The3 = 6 + 2 = 8
The4 = 8 + 2 = 10
The5= 10 + 2 = 12
The6 = 12 + 2 =14
This BP is equal to (4,6,8,10,12,14 …).
Do not stop now... There's more after the advertising ;)
General term of a PA
Describing the PA from a formula makes it easy for us to find any of its terms. To find any term of an AP, we use the following formula:
Theno=a1 + r·(n-1) |
N→ is the position of the term;
The1→ is the first term;
r → reason.
Example:
Find it general term of the PA (1,5,9,13,…) and the 5th, 10th and 23rd term.
1st step: find the reason.
To find the ratio, simply calculate the difference between two consecutive terms: 5 – 1 = 4; then, in this case, r = 4 .
2nd step: find the general term.
How do we know that the1= 1 and r = 4, let's substitute in the formula.
Theno=a1 + r (n - 1)
Theno=1 + 4 (n - 1)
Theno=1 + 4n - 4
Theno= 4n – 3 → general term of PA
3rd step: knowing the general term, let's calculate the 5th, 10th and 23rd term.
5th term → n = 5
Theno=4n - 3
The5=4·5 – 3
The5=20 – 3
The5=17
10th term → n = 10
Theno=4n - 3
The10=4·10 – 3
The10=40 – 3
The10=37
23rd term → n = 23
Theno=4n - 3
The23=4·23 – 3
The23=92 – 3
The23=89
Types of Arithmetic Progressions
There are three possibilities for a PA. It can be increasing, decreasing or constant.
Growing
As the name suggests, an arithmetic progression is increasing when, as the terms increase, their value also increases., that is, the second term is greater than the first, the third is greater than the second, and so on.
The1 < to2 < to3 < to4 < …. no
For this to happen, the ratio must be positive, that is, a PA is increasing if r > 0.
Examples:
(2,3,4,5,6,7,8,9 …)
(0,5,10,15,20,25...)
descending
As the name suggests, an arithmetic progression is descending when, as the terms increase, their value decreases, that is, the second term is less than the first, the third is less than the second, and so on.
The1 > the2 > the3 > the4 > …. >theno
For this to happen, the ratio must be negative, that is, a PA is increasing if r < 0.
Examples:
(10,9,8,7,6,5,4,3,2, …)
(0, -5, -10, -15, -20, …)
Constant
An arithmetic progression is constant when, as the terms increase, the value remains the same., that is, the first term is equal to the second, which is equal to the third, and so on.
The1 = the2 = the3 = the4 = …. =ano
For a PA to be constant, the ratio must be equal to zero, that is, r = 0.
Examples:
(1,1,1,1,1,1,1….)
(-2, -2 -2, -2, …)
See too: Product of the terms of a PG - what is the formula?
Properties of a PA
1st property
Given any term of a PA, the average arithmetic between its successor and predecessor is equal to that term.
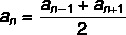
Example:
Consider the progression (-1, 2, 5, 8, 11) and the term 8. The average between 11 and 5 is equal to 8, that is, the sum of the successor with the predecessor of a number in the PA is always equal to this number.
2nd property
The sum of equidistant terms is always equal.

Example:
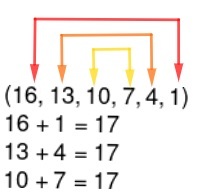
Sum of terms of a PA
Suppose we want to add the six BP terms shown above: (16,13,10,7,4,1). We can simply add their terms – in which case there are few terms, it's possible – but if it is a longer string, you should use the property. We know that the sum of equidistant terms is always equal, as we saw in the property, so if we perform this add once and multiply by half the amount of terms, we have the sum of the first six terms of the PAN.
Note that, in the example, we would be calculating the sum of the first and the last, which is equal to 17, multiplied by half the amount of terms, that is, 17 times 3, which is equal to 51.
The formula of sum of terms of a PA it was developed by the mathematician Gauss, who realized this symmetry in arithmetic progressions. The formula is written as follows:

sno → sum of n elements
The1 → first term
Theno → last term
n → number of terms
Example:
Calculate the sum of odd numbers from 1 to 2000.
Resolution:
We know that this sequence is an AP (1,3,5, …. 1997, 1999). Performing the sum would be a lot of work, so the formula is quite convenient. From 1 to 2000, half the numbers are odd, so there are 1000 odd numbers.
Data:
n→ 1000
The1 → 1
Theno → 1999
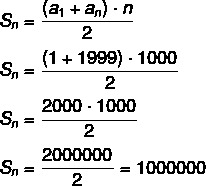
Also access: Sum of a finite PG – how to do it?
Interpolation of arithmetic means
Knowing two non-consecutive terms of an arithmetic progression, it is possible to find all the terms that fall between these two numbers, what we know as interpolation of arithmetic means.
Example:
Let's interpolate 5 arithmetic means between 13 and 55. That means there are 5 numbers between 13 and 55 and they form a progression.
(13, ___, ___, ___, ___, ___, 55).
To find these numbers, it is necessary to find the reason. We know the first term (the1 = 13) and also the 7th term (the7= 55), but we know that:
Theno = the1 + r ·(n – 1 )
When n = 7 → ano= 55. We also know the value of a1=13. So, substituting it in the formula, we have to:
55 = 13 + r ·( 7 – 1 )
55 = 13 + 6r
55 - 13 = 6r
42 = 6r
r = 42:6
r = 7.
Knowing the reason, we can find terms that are between 13 and 55.
13 + 7 = 20
21 + 7 = 27
28 + 7 = 34
35 + 7 = 41
41 + 7 = 49
(13, 20, 27, 34, 41, 49, 55)

solved exercises
Question 1 - (Enem 2012) - Playing cards is an activity that stimulates reasoning. A traditional game is Solitaire, which uses 52 cards. Initially, seven columns are formed with the cards. The first column has one card, the second has two cards, the third has three cards, the fourth has four cards, and so on successively to the seventh column, which has seven cards, and what makes up the pile, which are the unused cards in the columns.
The number of cards that make up the pile is:
A) 21.
B) 24.
C) 26.
D) 28.
E) 31.
Resolution
Alternative B.
First let's calculate the total number of cards that were used. We are working with an AP whose first term is 1 and the ratio is also 1. So, calculating the sum of the 7 rows, the last term is 7 and the value of n is also 7.

Knowing that the total number of cards used was 28 and that there are 52 cards, the pile is formed by:
52 - 28 = 24 cards
Question 2 - (Enem 2018) The city hall of a small town in the interior decides to put poles for lighting around the along a straight road that starts in a central square and ends in a farm in the area. rural. As the square already has lighting, the first pole will be placed 80 meters from the square, the second at 100 meters, the third at 120 meters, and so on. successively, always keeping a distance of 20 meters between the posts, until the last post is placed at a distance of 1,380 meters from the square.
If the city can pay a maximum of R$8,000.00 per post placed, the highest amount you can spend on placing these posts is:
A) BRL 512 000.00.
B) BRL 520,000.00.
C) R$528,000.00.
D) BRL 552,000.00.
E) BRL 584 000.00.
Resolution
Alternative C.
We know that posts will be placed every 20 meters, that is, r = 20, and that the first term of this PA is 80. Also, we know that the last term is 1380, but we don't know how many terms there are between 80 and 1380. To calculate this number of terms, let's use the general term formula.
Data: ano = 1380; The1=80; and r = 20.
Theno=a1 + r·(n-1)
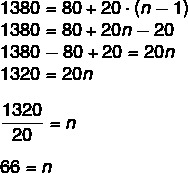
660 posts will be placed. If each one will cost a maximum of R$ 8,000, the highest amount that can be spent with the placement of these posts is:
66· 8 000 = 528 000
By Raul Rodrigues de Oliveira