The Cartesian plane is formed by two perpendicular axes that intersect at the origin of the coordinates (0,0), establishing four quadrants. The perpendicular intersection of the axes forms 90° angles. 
In the Cartesian plane, when we draw a straight line, which passes through the point (0,0) forming an angle of 45º with the abscissa (horizontal axis), we are dividing a quadrant in half and determining its bisector.
We can trace the bisectors of the quadrants in two ways: bisector of the even quadrants and bisector of the odd quadrants.
Bisector of odd quadrants
The bisector of the odd quadrants is determined by a straight line that intersects the point (0,0) tracing the bisectors of quadrants I and III. 
The slope will be equal to m = tg 45° = 1. One of its points will be (0,0) and all the other points belonging to the line b will have the ordinates and abscissa equal, for example, (4,4), (5,5), (6.6), (7, 7),...
Considering any of these points and the slope equal to 1, we can conclude that the line representing the bisector of odd quadrants will have - according to the concepts of Analytical Geometry - the fundamental equation: y – y0 = m (x – x0).
Replacing the point (2.2), we have:
y – 2 = 1 (x – 2)
y – 2 = x – 2
y = x
Bisector of the even quadrants
The bisector of the even quadrants is determined by a straight line that intersects the point (0,0) tracing the bisectors of quadrants II and IV.
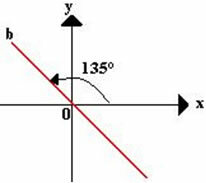
The slope will be equal to m = tg 135° = -1. One of its points will be (0,0) and all other points belonging to the line b will have the ordinate values opposite to the abscissa values, for example, (4,-4), (5,-5), (6, -6), (7,-7),...
Considering any of these points and the slope equal to -1, we can conclude that the line representing the bisector of the even quadrants will have - according to the concepts of Analytical Geometry - the fundamental equation: y – y0 = m (x – x0).
y – (–2) = –1 (x – 2)
y + 2 = –x + 2
y = - x
Do not stop now... There's more after the advertising ;)
by Mark Noah
Graduated in Mathematics
Brazil School Team
Analytical Geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "The bisectors of the quadrants"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/as-bissetrizes-dos-quadrantes-1.htm. Accessed on June 28, 2021.



