We call the set of linear equations in variable x with m equations and n variables a linear system. When solving a linear system we can obtain the following solution conditions: a single solution, infinite solutions or no solution.
Possible and Determined System (SPD): when solved we will find a single solution, that is, only a single value for the unknowns. The following system is considered a possible and determined system, as the only existing solution for it is the ordered pair (4,1). 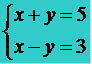
Possible and Indeterminate System (SPI): this type of system has infinite solutions, the values of x and y take on countless values. Note the following system, x and y can take on more than one value, (0.4), (1.3), (2.2), (3.1) and so on. 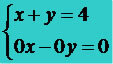
Impossible System (SI): when solved, we will not find possible solutions for the unknowns, so this type of system is classified as impossible. The system to follow is impossible. 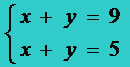

by Mark Noah
Graduated in Mathematics
Brazil School Team
Matrix and Determinant - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/classificacao-um-sistema-linear.htm
