we call cone a geometric solid, also known as a round body or solid of revolution, which it has a circular base and is constructed from the rotation of a triangle.. The cone and other geometric solids are objects of study of spatial geometry. According to its characteristics, it can be classified as:
- straight cone;
- oblique cone;
- equilateral cone.
There is specific formulas for calculating the total area and volume of the cone.
Read too: What are geometric shapes?
Icon elements
the cone is a solid geometric known as revolution solid. Very present in our daily lives, it is known as a solid of revolution for being built from the rotation of a triangle.
Its base is always a circle. In addition to the base itself, another important element is the lightningr of the circumference, known as the radius of the base of the cone. Also, there is the vertex of the cone (V) and the height (h), which, by definition, is the segment that leaves the vertex and is perpendicular to the base, that is, it forms an angle of 90º.

In addition to the elements already mentioned, there is another important element in the cone, which is the generatrix. We call any segment that starts from the vertex and meets the circumference from the base.
The generatrix is the AV line segment in the image. Note that he is the hypotenuse of the stroke triangle, soon we can establish a relationship Pythagorean between radius, height and generatrix.
g² = r² + h²

g → cone generator
r→ base radius
H→ height
See too: What are the applications of Pythagoras' theorem?
Icon classification
According to its characteristics, we can classify the cone in two cases: straight or oblique. As a particular case of a straight cone, there are equilateral cones.
oblique cone
A cone is known as oblique when the segment connecting the vertex with the center of its base does not match the height of the cone.

When the vertex is not aligned with the center of the base, the segment that connects the vertex to the center of the circumference it is no longer the height as in the straight cone. note that the axis of the cone, in the image, is not perpendicular to the base. In this case, their generatrices are not all congruent, so it is not possible to find their length by Pythagoras' theorem, with no specific formulas for the generatrix or for the volume and its area overall.
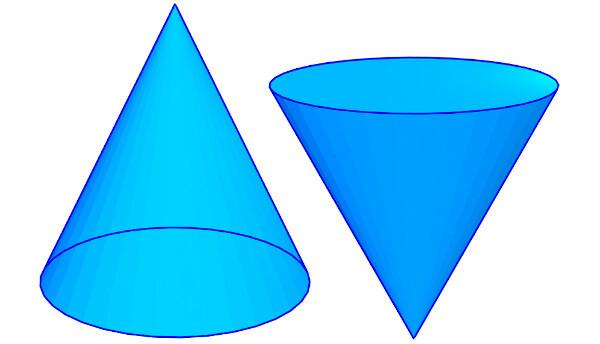
straight cone
The cone is known as a straight when its axis coincides with the height of the cone, that is, the segment that connects the vertex to the center of the base circumference is perpendicular to the plane that contains the base of the cone.

equilateral cone
A straight cone is known as equilateral when its diameter is equal to its generatrix.

Note that the AVB triangle is an equilateral triangle, that is, all sides are congruent, which means that its generatrix is congruent to the diameter of the base and that, consequently, the length of the generatrix is equal to twice the length of the radius of the base.
Also access: Conics – figures formed by the intersection of a plane and a double cone
Cone formulas
When studying geometric solids, there are two important calculations for each of them, which is the volume calculation and the calculation of the total area of the geometric solid. To calculate the value of cone volume of each of them, it is necessary to use specific formulas. Remember that these formulas are specific to the straight cone.
Cone volume formula

r → base radius
V→ volume
h → height
Total cone area formula
To calculate the total area, analyzing the planning of the cone, we will sum the lateral area with the base area of a cone.
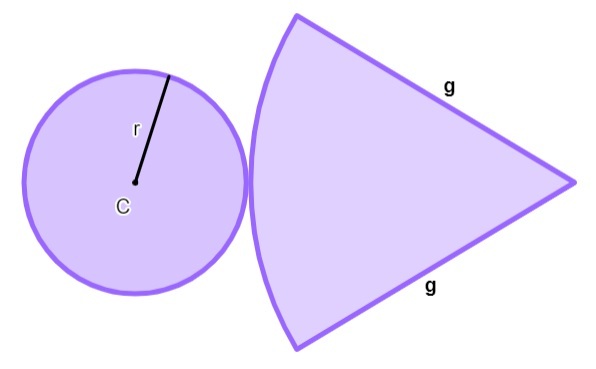
Its base is a circle, so the area is calculated by:
THEB = π·r².
Its side area is a circular sector, which is equal to:
THEthere = π·r·g
Therefore, the total area is equal to:
THEt = π·r² + π·r·g
Putting π·r in evidence, we can calculate the total area by:
THEt = π·r (r+g)
r→ radius
g → generatrix
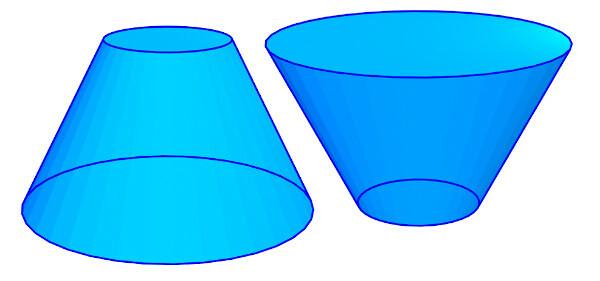
cone trunk
When a cone is intersected by a plane parallel to the base, it is possible to create the geometric solid known as the trunk of a cone. O trunk of a cone will always have two bases in the shape of circles, one bigger and the other smaller.
Read too: Cylinder - solid formed by two circular bases in distinct and parallel planes
solved exercises
Question 1 - (Enem 2013) A cook, specialist in baking cakes, uses a mold in the format shown in the figure:
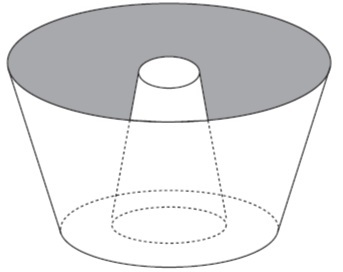
It identifies the representation of two three-dimensional geometric figures. These figures are:
A) a frustum of cone and a cylinder.
B) a cone and a cylinder.
C) a trunk of a pyramid and a cylinder.
D) two cone trunks.
E) two cylinders.
Resolution
Alternative D. Note that the two solids have a larger base and a larger circular base, which makes them both frusto-conical.
Question 2 - A reservoir will be built in the shape of a cone, using aluminum as the material. Disregarding the thickness of the reservoir and knowing that it is a straight cone with 1.5 m radius and 2 m high, what is the amount of aluminum needed to build this reservoir? (use π = 3)
A) 10 m²
B) 14 m²
C) 16 m²
D) 18 m²
E) 20 m²
Resolution
Alternative D.
We want to calculate the total area of the cone, which is given by:
THEt = π·r (r+g)
Note that we don't have the value of g, so first let's calculate the value of the generatrix g.
g² = r² + h²
g² = 1.5² + 2²
g² = 2.25+4
g² = 6.25
g = √6.25
g = 2.5 m
So the total area will be:
THEt = π·r (r+g)
THEt = 3·1,5(1,5+2,5)
THEt = 4,5·4
THEt = 18 m²
By Raul Rodrigues de Oliveira
Maths teacher

