Thales' Theorem has several applications in everyday life, which must be demonstrated in order to verify its importance. The Theorem says that "parallel lines, cut by transverses, form corresponding proportional segments". Through applied exercises we will understand the Theorem. We can demonstrate the Theorem through a generalization, where the lines r, s, x are parallel and the lines t and w are transversal. Look:

By theorem we have to
Example 1
When analyzing the plan of a block of a given condominium, the engineer found the absence of some measurements on the boundaries of certain residential lots. He needs to calculate these measurements from his own office, based on the plant information. Note the detailed drawing of the situation:
Do not stop now... There's more after the advertising ;)
Based on the plan, we must calculate the x and y sides of the lots. Note that the sides of lots 1, 2 and 3 are perpendicular to streets A and B. The plant satisfies the Thales relation, so we can use the Theorem.

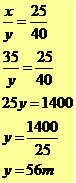
Example 2
When performing the electrical installation of a building, an electrician observed that the two wires r and s were transversal to the wires of the central network shown by a, b, c, d. Knowing this, calculate the length x and y of the figure.
Note: the central network wires are parallel.
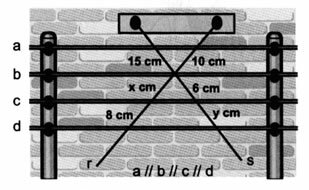
Applying Thales' Theorem, we have:

by Mark Noah
Graduated in Mathematics
Brazil School Team
plane geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Applications of Thales' Theorem"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/aplicacoes-teorema-tales.htm. Accessed on June 27, 2021.