The study of trigonometry allows the determination of sine, cosine and tangent values for different angles based on known values. At arc addition formulasare one of the most used for this purpose:
sin (a + b) = sin a · cos b + sin b · cos a
sin (a – b) = sin a · cos b – sin b · cos a
cos (a + b) = cos a · cos b – sin a · sin b
cos (a – b) = cos a · cos b + sin a · sin b
tg (a + b) = tg a + tg b
1 - tg a · tg b
tg (a - b) = tg a - tg b
1 + tg a · tg b
From these formulas, it is simple to determine how to proceed when the angles The and B they are the same. In this case, we say that it is about the trigonometric functions of the double arc. Are they:
sin (2a) = 2 · sin a · cos a
cos (2a) = cos² a - sin² a
tg (2a) = 2 · tg a1 - tg² to
From these functions, we will determine the trigonometric functions of the arc half. Consider the following trigonometric identity:
sin² a + cos² a = 1
sin² a = 1 - cos² a
let's replace sen² to in cos (2a) = cos² a - sin² a:
cos (2a) = cos² a - sen² to
cos (2a) = cos² a - (1 - cos² a)
cos (2a) = cos² a - 1 + cos² a
cos (2a) = 2 · cos² a – 1
Do not stop now... There's more after the advertising ;)
But we are looking for the right formula for the half bow. To do so, consider that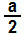 
it's half the arc The, and wherever there is 2nd, we will only use The:
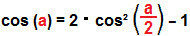
isolating the cos² (The/2):
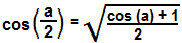
Then we have the formula for calculating the cosine of arc half. From it we will determine the sine of 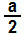. From the trigonometric identity, we have:
sin² a + cos² a = 1
cos² a = 1 - sin² a
replacing cos² a in the formula of the cosine of the double arc, cos (2a) = cos² a - sin² a, we will have:
cos (2a) = cos² a – sen² to
cos (2a) = (1 - sen² a) – sen² to
cos (2a) = 1 – 2 · sin² a
Again, let us consider half of the arcs in cos (2a) = 1 – 2 · sin² a. It will then remain:
isolating the sen² (The/2), we will have:
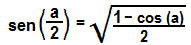
Now that we've also found the formula for sine of the arc half, we can determine the tangent of 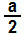. Soon:
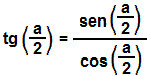
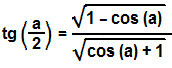
We have then determined the formula for calculating the half arc tangent.
By Amanda Gonçalves
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
RIBEIRO, Amanda Gonçalves. "Trigonometric functions of the half arc"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/funcao-trigonometrica-arco-metade.htm. Accessed on June 27, 2021.
trigonometry, trigonometric functions, what is double arc, double arc, arc, calculation of double arc, calculation of trigonometric functions, calculation of trigonometric functions of double arc.
Trigonometry, trigonometric function, addition, subtraction, arc addition formulas, arc of a circle, circle, arc, sine, cosine, tangent.
function, trigonometric function, tangent, cosine, sine, cosecant, cotangent, arc, angles, arc value, trigonometric function value, relationship between angle and trigonometric function.
