THE radiciation, as well as all the operations of the set of real numbers, have your reverse, that is, when we take an element and operate with its inverse, the result is equal to the neutral element.
THE addition has the subtraction as a reverse operation, the multiplication has the division as an inverse operation, and the potentiation will also have its inverse operation, which is called radiciation.
Like other operations, rooting also has a series of properties, let's see.

Radiation representation
Radiciation is an operation in which we look for a number that satisfies certain potency. consider the numbers The and B real numbers and no a number rational, we define the nth root of The as being a number that, when raised to no, be equal to the number The, in this case, represented by B, i.e:

Examples
a) The square root of 36 is equal to 6, since 62 = 36.
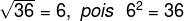
Note that to determine the square root of 36, we must look for a number that, when we squared, is equal to 36. Of course, that number is 6.
b) The cubic root of 125 is equal to 5, since 53 = 125.
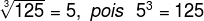
c) Now let's look at the tenth root of 1024. As this is not a trivial number, the best way out is to perform the prime factor decomposition of the 1024 and then write it in the power form.

See that the number 1024 = 210, so the number that, raised to the 10th power, results in 1024 is the number 2, that is:

Do not stop now... There's more after the advertising ;)
Radiciation nomenclature

Considering the previous nth root, we have the following nomenclature:
a → Rooting
n → index
b → root
√ → Radical
Radiation properties
Just like in potentiation, we have some properties on radiciation. In this one, the story is the same, since both are reverse operations.
Property 1: Root where the exponent of the radicand is equal to the index
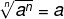
Property 1 states that, whenever the index is equal to the exponent of the radicand, the result of the nth root is the base itself.
Examples
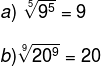
Property 2: radical exponent power
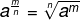
Property 2 is actually an enhancement property where the exponent is a fraction. The numerator of fraction becomes the exponent of the radicand, and the denominator becomes the index of the root. See an example:

Read too: Powers of base 10 — the foundation of scientific notation
Property 3: Equal Index Root Product

Property 3 states that the product between two roots with equal indices is equal to the root of the same index of the product of radicands.
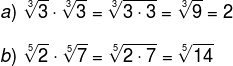
Property 4: Ratio of roots of equal indexes

Analogously to property 3, property 4 states that the division between two roots of equal indices is equal to the root of the same index of the division of the quotients.
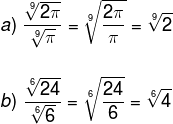
See too: Square root: rooting with index 2
Property 5: potency of a root
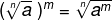
Property 5 tells us that an nth root raised to a given exponent m is equal to the nth root of the radicand to the exponent.
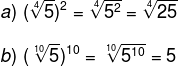
Property 6: root of another root
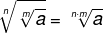
When we come across a root of another root, just keep the root and multiply the root indices.
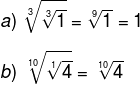
Property 7: Root simplification
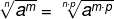
Property 7 states that, in an nth root of a power, we can multiply the index and exponent of the radicand by any number as long as it is different from 0.
Also access: Radical reduction at the same index
solved exercises
question 1 – Find the square root of 1024.
Solution
In the text example, we have the factorization of the number 1024, which is given by:
1024 = 210
1024 = 2 (5 · 2)
1024 = (25)2
So the square root of 1024 is:
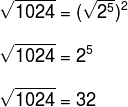
question 2 – (Enem) The skin that covers the body of animals plays an active role in maintaining body temperature, in elimination of toxic substances generated by the body's own metabolism and protection against environmental aggressions outside.
The following algebraic expression relates to mass. (m) in kg of an animal with your size (THE) of body surface in m2, and k it's a real constant.
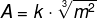
The real constant k varies from animal to animal, according to the table:
Animal |
Man |
Monkey |
Cat |
Ox |
Bunny |
Constant K |
0,11 |
0,12 |
0,1 |
0,09 |
0,1 |
Consider an animal with 27 kg of mass and a body area of 1,062 m2.
According to the table presented in the statement, this animal is more likely to be a:
a) man.
b) monkey.
c) cat.
d) ox.
e) rabbit.
Solution
Alternative b
Substituting the data in the formula given in the statement and writing 27 = 33, we have:
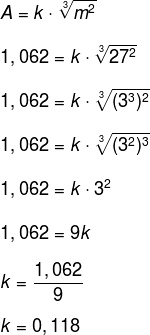
Therefore, the animal in question is more likely to be the ape.
by Robson Luiz
Maths teacher