Imagine playing with marbles to form triangles. You can first consider that a ball is like a small triangle:
•
Then you place two marbles below them and form the three vertices of a triangle:
•
• •
If you place another three balls below these, it will form another triangle:
•
• •
• • •
At each step of adding balls in relation to the amount previously placed, there will always be the formation of triangles. See the triangle formed by adding four more balls:
•
• •
• • •
• • • •
The total number of balls in each step characterizes a class of numbers called the triangular numbers. The mathematician Karl Friedrich Gauss discovered a formula to indicate the total amount in each triangle, where s1corresponded to the first triangle, s2, to the second triangle, and so on. The sums described by Gauss started with a and, at each stage, a number was added that corresponded to one unit above the last number added:
s1 = 1
s2= 1 + 2 = 3
s3 = 1 + 2 + 3 = 6
s4= 1 + 2 + 3 + 4 = 10
s5 = 1 + 2 + 3 + 4 + 5 = 15
The results of these sums were the triangular numbers: 1, 3, 6, 10, 15... Note that there is a pattern established in each of these sums. Looking carefully, we can see that each one of them is a
arithmetic progression of reason 1. So here is the gauss sum, which establishes that, in a constant ratio sum, if we add the first element to the last, we will obtain the same result as adding the second element to the penultimate one. Let's see how the Gauss sum process for sums occurs. s6 and s7: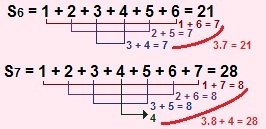
Gauss sum process applied to the sum of triangular numbers
Do not stop now... There's more after the advertising ;)
if stop s6 and s7 we have the sums from the image above, let's reproduce this sum for s8, S9, S10 and s11:
s8 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 4.9 = 36
s9= 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 4.10 + 5 = 45
s10= 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 5.11 = 55
s11= 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11= 5.12 + 6 = 66
We can generalize to get a sum for sno:
sno = n. (n+1), if n is even
2
sno = (n - 1).(n+1) + (n - 1) + 1, if n is odd
2 2
just like in number magic, we can show another interesting fact about triangular numbers: the sum of subsequent triangular numbers always results in numbers that can be classified as perfect squares, that is, numbers that have root square. Let's see:
s1 + S2 = 1 + 3 = 4
s2 + S3 = 3 + 6 = 9
s3 + S4 = 6 + 10 = 16
s4 + S5 = 10 + 15 = 25
s5 + S6 = 15 + 21 = 36
s6 + S7 = 21 + 28 = 49
s7 + S8 = 28 + 36 = 64
s8 + S9 = 36 + 45 = 81
s9 + S10 = 45 + 55 = 100
s10 + S11 = 55 + 66 = 121
The results obtained, 4, 9, 16, 25, 36, 49, 64, 81, 100 and 121, are all perfect squares.
By Amanda Gonçalves
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
RIBEIRO, Amanda Gonçalves. "Triangular Numbers"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/numeros-triangulares.htm. Accessed on July 27, 2021.

