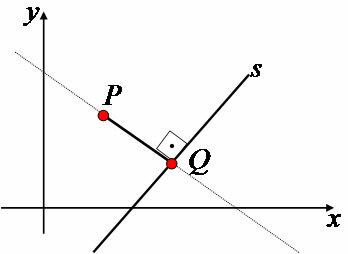
Given any point P with coordinates (x0,y0) common to two lines r and s, we say that the lines are concurrent in P. Thus, the coordinates of point P satisfy the equation of lines r and s.
given the straights a: the1x + b1y + c1 = 0 and s: the2x + b2y + c2 = 0, they will be competitors if they satisfy the condition established by the following square matrix: 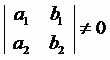 .
.
Thus, two lines will be concurrent if the matrix formed by its coefficients a and b result in a determinant other than zero.
Example 1
Check if the straight r: 2x - y + 6 = 0 and s: 2x + 3y – 6 = 0 are competitors.
Resolution:

The determinant of the matrix of coefficients of the lines r and s resulted in the number 8, which is different from zero. Therefore, the straights are competitors.
Determining the coordinate of the intersection point of the lines
To determine the coordinate of the intersection point of the lines, just organize the equations of the lines in a system of equations, calculating the values of x and y, using the solving method of substitution or addition.
Example 2
Let's determine the coordinates of the intersection points of the lines r: 2x – y + 6 = 0 and s: 2x + 3y – 6 = 0.
arranging the equations
r: 2x – y + 6 = 0 → 2x – y = –6
s: 2x + 3y – 6 = 0 → 2x + 3y = 6
Assembling the system of equations:
Do not stop now... There's more after the advertising ;)

Solving the system by the replacement method
1st equation - isolate y
2x – y = –6
–y = – 6 – 2x (multiply by –1)
y = 6 + 2x
2nd equation - replace y by 6 + 2x
2x + 3y = 6
2x + 3(6 + 2x) = 6
2x + 18 + 6x = 6
2x + 6x = 6 - 18
8x = – 12
x = -12/8
x = – 3/2
Determining the value of y
y = 6 + 2x
y = 6 + 2*(–3/2)
y = 6 - 6/2
y = 6 - 3
y = 3
Therefore, the coordinates of the intersection point of the lines r: 2x – y + 6 = 0 and s: 2x + 3y – 6 = 0 is x = -3/2 and y = 3.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Analytical Geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Two straight line competition condition"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/condicao-concorrencia-duas-retas.htm. Accessed on June 29, 2021.