A monomium, or an algebraic term, is an entire algebraic expression composed of a literal part and a numerical coefficient, that is, letters and numbers. We say that it is integer because it cannot show the presence of variables inside radicals or even in fraction denominators. For example, 2x is a monomial, and 2 is your coefficient and x it's your literal part. 5ab2 it is also a monomial, since 5 is the coefficient, and the literal part is ab2.
Another common case of monomials is the form X Y Z. We have a clear vision that X Y Z is the literal part, but in this case the numerical coefficient is not clear, but it is present and it is the number 1. We could rewrite this monomium in the form 1xyz.
There are still cases in which the literal part is not included, only the numerical coefficient appears, which characterizes a monomial without literal part. Any real number can be classified this way. If we only have the number zero and let's not have the literal part, we say it's a null monomium.
If two or more monomials have the same literal part, it is similar monomials or similar terms. For example, the monomials x, 2x and √3x they are all similar monomials, as they all have the same literal part. x. Among similar monomials, we can add and subtract as we will see below:
Below are three addition operations performed between monomials.

When adding monomials, we must add the coefficients and repeat the literal part
Do not stop now... There's more after the advertising ;)
To perform them, just add the coefficients and repeat the literal part. If the monomials in question are not similar, there is no sum. For example, the sum of 2x and 3y simply results in 2x + 3y, a binomial, as there is the addition of two monomials that are not similar. If we add three monomials that are not similar, we will have the formation of a trinomial. For the addition or subtraction of four or more monomials that are not similar, there is a polynomial. The calculation of addition, subtraction and multiplication of polynomials it is very similar to performing these calculations with monomials.
The way to perform the subtraction of similar monomials is analogous to addition. We must subtract the coefficients and repeat the literal part, as we can see below:

To subtract similar monomials, we subtract the coefficients and repeat the literal part.
To perform the multiplication, division and potentiation of monomials, it is not necessary for them to be similar. For these operations, it is enough to operate the coefficients between themselves and the literal part of one by the literal part of the other. Here are some examples:
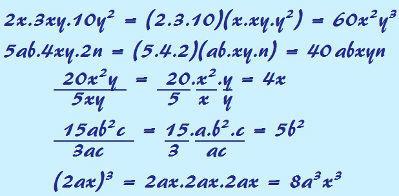
To perform the operations of multiplication, division and potentiation of monomials, it is not necessary for the monomials to be similar
By Amanda Gonçalves
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
RIBEIRO, Amanda Gonçalves. "What is Monomium?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-monomio.htm. Accessed on June 27, 2021.
Learn the definition of polynomial equation, define a polynomial function, the numerical value of a polynomial, the root or zero of the polynomial, Degree of a polynomial.