When we measure the angle of an arc, we use the degree or the radian as a unit. We have that 1st (one degree) has 60’ (sixty minutes) and 1’ (one minute) has 60” (sixty seconds). A circle has 360 arcs of 1° opening. In the case of measuring in radians, we say that the arc measures one radian (1 rad) if its length is equal to the length of the radius of the circumference where the measured arc is.
The following table shows some relationships between the units in degrees and radians.

Converting Degrees to Radians
In converting degrees to radians we use a simple rule of three, for example:
20th in radians
| degrees | radians |
| 20º | x |
| 180º | rad |

15th in radians
| degrees | radians |
| 15º | x |
| 180º | rad |
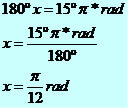
120º in radians
| degrees | radian |
| 120º | x |
| 180º | rad |

150º in radians
| degrees | radian |
| 150º | x |
| 180º | rad |

300º in radians
| degrees | radian |
| 300º | x |
| 180º | rad |

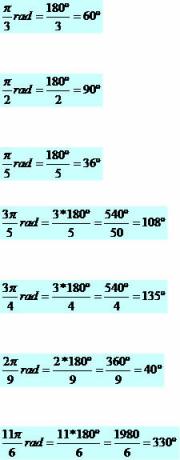
Converting Radians to Degrees
In converting radians to degrees, we just replace the value of π by 180º. See examples:
by Mark Noah
Graduated in Mathematics
Brazil School Team
Trigonometry - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/conversoes-medidas-angulos.htm
