Algebraic expression factorization. Algebraic Factorization Methods

THE algebraic expression factorization consists of writing an algebraic expression in product form. In practical cases, that is, in the solution of some problems that involve algebraic expressions, factorization is extremely useful because, in most situations, it simplifies the worked expression.

To perform factorization of algebraic expressions, we will use a very important result in mathematics called fundamental theorem of arithmetic, which states that any integer greater than 1 can be written as the product of Prime numbers, Look:

121 = 11 · 11

60 = 5 · 4 · 3

We just factored out the numbers 121 and 60.

Read too: Decomposition of a number into prime factors

Methods for Factoring Algebraic Expressions

Now we will see the main factorization methods, the most used ones we will do a brief geometric justification. Look:

• Evidence factoring

Consider the rectangle:

Note that the rectangle blue plus the area of ​​the green rectangle results in the larger rectangle. Let's look at each of these areas:

THE_BLUE = b · x

THE_GREEN = b · y

THE_BIGGER = b · (x + y)

So, we have to:

THE_BIGGER = A_BLUE + A_GREEN

b (x + y) = bx + by

• Examples

The) To factor the expression: 12x + 24y.

Note that 12 is the factor in evidence, since it appears in both parcels, so to determine the numbers that go inside the parentheses, it is enough share each parcel by the factor in evidence.

12x: 12 = x

24y: 12 = 2y

12x + 24y = 12 · (x + 2y)

B) To factor expression 21ab² – 70th²B.

In the same way, initially, the factor in evidence is determined, that is, the factor that is repeated in the parcels. See that from the numerical part we have the 7 as a common factor, since it is the one that divides both numbers. Now, regarding the literal part, see that only the factor is repeated ab, therefore, the factor in evidence is: 7ab.

21ab² – 70th²b = 7ab (3b - 10^The)

Read too: Polynomial division: how to do it?

• Factoring by grouping

The factorization by grouping is arising from factoring by evidence, the only difference is that, instead of having a monomium as a common factor or a factor in evidence, we will have a polynomial, see the example:

Consider the expression (a + b) · xy + (a + b) · wz²

Note that the common factor is the binomial (a + b),therefore, the factored form of the previous expression is:

(a + b) · (xy + wz²)

• difference between two squares

Consider two numbers a and b, when we have a difference of the square of these numbers, that is, the² - B², so we can write them as the product of sum for difference, i.e:

The² - B² = (a + b) · (a - b)

• Examples

The) To factor the expression x² - y².

We can use the difference between two squares, so:

x² - y² = (x + y) · (x - y)

B) To factor 2020² – 2.019².

We can use the difference between two squares, so:

2.020² – 2.019² = (2.020 + 2.019) · (2.020 – 2.019)

2.020² – 2.019² = 4.039 · 1

2.020² – 2.019² = 4.039

• Trinomial of the perfect square

Take the next square from the side (a + b) and note the areas of the squares and rectangles formed inside it.

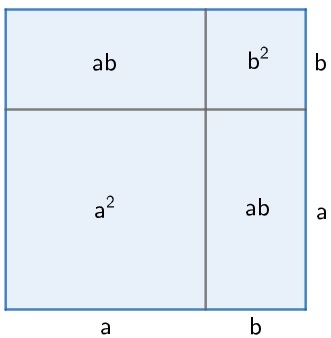
See the area of square greater is given by (a + b)², but, on the other hand, the area of ​​the largest square can be obtained by adding the squares and rectangles inside it, like this:

(a + b)² = the²+ ab + ab + b²

(a + b)² = the²+ 2b + b²

(a + b)² = the² + 2ab + b²

Similarly, we have to:

(a - b)² = the² – 2ab + b²

• Example

Consider the expression x² + 12x + 36.

To factor an expression of this type, just identify the coefficient of variable x and the independent coefficient, and compare with the given formula, see:

x² + 12x + 36

The² + 2ab + b²

Making the comparisons, see that x = a, 2b = 12 and b² = 36; of the equalities, we have that b = 6, so the factored expression is:

x² + 12x + 36 = (x + 6)²

• High School Trinomial

Consider the ax trinomial² + bx + c. Its factored shape can be found using your roots, that is, the values ​​of x that zero out that expression. To determine the values ​​that make this expression zero, just solve the equation ax² + bx + c = 0 using whatever method you find convenient. Here we highlight the best known method: Bhaskara method.

The factored form of the ax trinomial² + bx + c is:

ax² + bx + c = a · (x – x₁) · (x - x₂)

• Example

Consider the expression x² + x – 20.

The first step is to determine the roots of the x equation.² + x – 20 = 0.

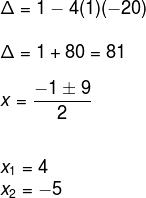
So the factored form of the expression x² + x – 20 is:

(x – 4) · (x + 5)

• Cube of the difference between two numbers

The cube of the difference between two numbers a and b is given by:

(a - b)³ = (a – b) · (a - b)²
(a - b)³ = (a – b) · (a² – 2ab + b²)

• Cube of the sum of two numbers

Similarly, we have that (a + b)³ = (a + b) · (a + b)² , soon:

(a + b)³ = (a + b) · (a² + 2ab + b²)

Factorization is an instrument that facilitates the resolution of algebraic expressions.

solved exercises

question 1 – (Cefet-MG) Where the number n = 684² – 683², the sum of the digits of n is:

a) 14

b) 15

c) 16

d) 17

e) 18

Resolution

Alternative d. To determine the sum of the digits of n, we first factor the expression, since calculating the squares and then subtracting is unnecessary work. Factoring the expression using the difference between two squares, we have:

n = 684² – 683²

n = (684 + 683) · (684 - 683)

n = 1,367 · 1

n = 1,367

Therefore, the sum of the digits of n is given by 1 + 3 + 6 + 7 = 17

Question 2 - (Modified Insper-SP) Determine the value of the expression:

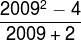
Resolution

In order to make the notation easier, let's name a = 2009 and b = 2. remember that 2² = 4, so we have to:

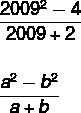
Notice that, in the numerator of the fraction, we have the difference between two squares, so we can write the² - B² = (a + b) (a – b). Soon:

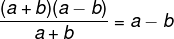
a – b = 2009 – 2 = 2007.

by Robson Luiz
Maths teacher

Source: Brazil School - https://brasilescola.uol.com.br/matematica/fatoracao-expressao-algebrica.htm