Fraction it is the representation of a part of something whole, as with the apples shown in the previous figure. Thus, we can say that the fraction represents a quantity, that is, a numerical form. This being then a number, it is possible to consider the basic operations of mathematics, such as addition, subtraction, multiplication, division, potentiation and radiciation.
The numerical set in which the fractions are contained is called the set of rational numbers,which is generally represented as follows:
We name the upper part, here represented by the letter The, in numerator, and the bottom, here represented by B, in denominator.
Read too: Whole number operations: learn how to do it
How to represent a fraction

Representing a fraction is quite simple, the denominator indicates how many parts the whole part has been divided into, and the numerator indicates how many parts we consider.
- Example
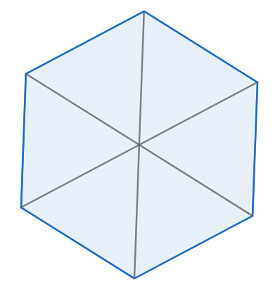
Note that, in example 1, the hexagon was divided into six equal parts, that is, each part equals one sixth of the total.

In example 2, the circle was divided into four equal parts, that is, each part equals a quarter of the total.
See too:Three Common Mistakes in Algebraic Fraction Simplification
equivalent fraction
We say that two or more fractions are equivalent when they represent the same amount. For the process of checking between two or more fractions to determine whether or not they are equivalent, simply multiply or divide the numerator and denominator by a number other than 0.
When we apply the division operation on the numerator and denominator, the process is called simplification.
- Example
Let's determine the equivalent fractions of 1 on 2, 1 .
2
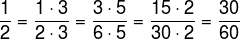
Note that we multiply both the numerator and denominator by the same number over and over again. At each step, both are multiplied by 3, 5 and 2. We can choose any number to multiply or divide, so we always find a new equivalent fraction.

Notice that when we take two parts of the circumference that has been divided into four equals to take half of the entire circumference.

I.e:
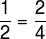
Operations with fractions
- Addition or subtraction of fractions
To add or subtract two or more fractions, just perform the Minimum Common Multiple - MMC of the denominators and then divide the MMC by the denominator of each fraction and multiply the result by the numerator. See an example:

To learn more about this subject, read our text: Fraction addition and subtraction.
- Fraction multiplication
To multiply two or more fractions, simply multiply the denominators and numerators.

If you want to know more about this topic, read our text: Multiplication with fraction.
- Fraction division
To divide between two or more fractions, just keep the first fraction and multiply it by the inverse of the second.
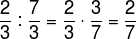
If you are more interested in this subject, read: Division with fraction.
- Potentiation or Fraction Radiation
To calculate the power or root of a fraction, just calculate separately the power or root of the numerator and then the denominator.

by Robson Luiz
Maths teacher

