parallel lines are those that do not intersect at any point. A line is transversal to the other if both have only one point in common. When we draw two straight lines r and s, such that r // s (“r is parallel to s”), and also a transverse line t intercept r and s, there will be the formation of eight angles. In the following image, we identify these angles by a, b, c, d, e, f, g, h.
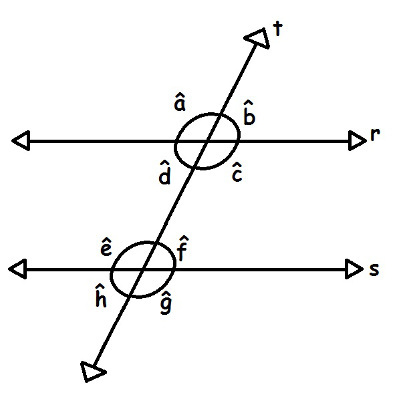
The intersection of the line t with the parallel lines r and s gave rise to angles a, b, c, d, e, f, g, h
Try drawing a drawing similar to the one shown of two parallel lines cut by a cross. When you finish your drawing, divide it in half, cutting it between the parallel lines. If you put the angles formed by the lines s and t exactly on top of the angles formed by the straight lines r and s, you will notice that they are exactly the same.
We can classify the angles formed by two parallel lines cut by a transversal one according to the position of these angles. if they are between the parallel lines, we say these angles are
internal; otherwise we say they are external. In the following figure, the outside angles are in the blue band, while the inside angles are in the yellow band. When analyzing two angles, they can be on the same side or on alternate sides in relation to the transversal line. If two angles are to the right or both are to the left of the line t, we say that these angles are collaterals; but if they are on alternate sides, one on the right and one on the left, we say that these angles are alternates.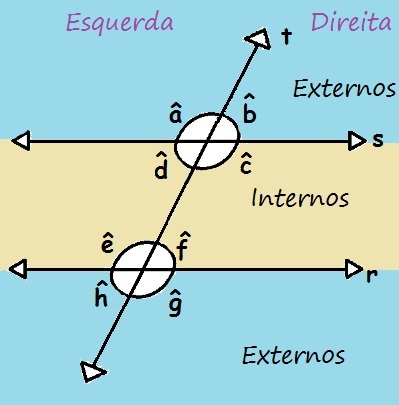
Angles can be classified as internal or external, and two angles can be collateral or alternate
Knowing that the angles formed by straight lines r and t are the same as those formed by the lines s and t, we can say that the pairs of angles below are correspondents:
The and and
B and f
ç and g
d and H
These pairs of corresponding collateral angles mentioned above have the same measurement. But we know that the angles opposite by the vertex are congruent, that is, they also have the same measure. So, we can say that:
- The =c = e = g
- b = d = f = h
the angles d and f and also and and ç can be classified as internal alternating angles, as they are in the inner region and on alternate sides. the angles d and and, as well as the ç and f, can be classified as internal side angles, since they are in the inner region and on the same side in relation to the line t.
Similarly, the angles The and H, as B and g, they are external side angles, as they are in the external region and on the same side in relation to the line t. just like the angles The and g, as well as B and H, they are external alternating angles, as they are in the external region and on alternate sides in relation to the transversal line t.
In the following figure, we can clearly see the alternating angles inside, inside collaterals, external alternates and external collaterals formed by two parallel lines cut by a cross:
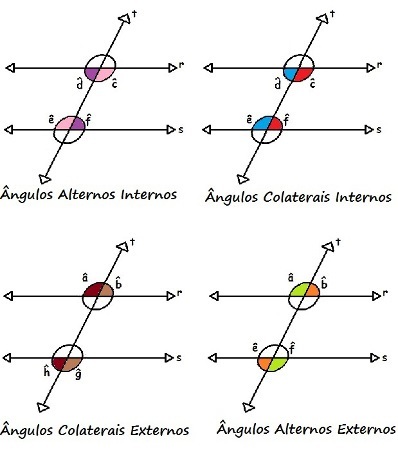
Two parallel lines cut by a transverse form alternate internal angles, internal collaterals, external alternatives and external collaterals
By Amanda Gonçalves
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/retas-paralelas-cortadas-por-uma-transversal.htm
