One Ellipse is a flat geometric figure obtained by the intersection between a flat it is a cone. That's why this figure is called conical, just like the circumference, a parable and the hyperbole. The following figure is an example of an ellipse and demonstrates the difference between the geometric representation of this figure and the circumference.

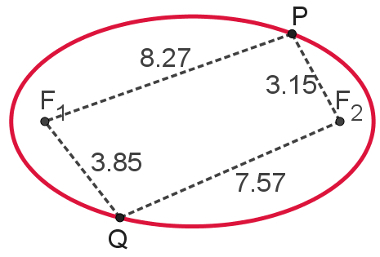
In the figure above, the F points1 and F2 they are focusesgivesEllipse, and the distance between them is defined as 2c.
Formal definition of the ellipse
Given the F points1 and F2, with the distance 2c between them, the Ellipse it's the setFrompoints P where the following equality is valid:
dPF1 + dPF2 = 2nd
In other words, the Ellipse is the set of points in which the sumof thedistances even each of focuses is equal to constant 2a. Thus, we can say that P is a point belonging to an ellipse if the sum of the distances from P to each of the foci is equal to 2a.
The following image illustrates this definition. Note that the sumof thedistances between P and the
focuses gives Ellipse is equal to the sum of the distances from point Q to the focus of the ellipse. Therefore, P and Q belong to this ellipse.Note that length 2a is always greater than length 2c.
Ellipse Elements
Below, check out a list of the main elementsgivesEllipse and a brief definition of each of them.
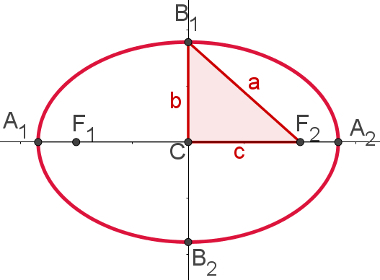
Spotlights: in the images in this article, the focuses are the F points1 and F2. These are key points at which distances must be evaluated to know whether a point belongs or does not belong to the ellipse.
center: given the F focuses1 and F2, the center of the ellipse is the midpoint of the segment F1F2 whose ends are the foci.
Axlebigger: in the image below, the major axis is segment A1THE2. Their endpoints are points that belong to the intersection between the ellipse and the line containing the foci. The measure of this axis is equal to 2a, the same length as the sum of the distances between any point on the ellipse and its foci.
Axlesmaller: in the image below, the minor axis is segment B1B2. Their endpoints are points that belong to the intersection between the ellipse and the straight line perpendicular to the major axis. The length of this axis is equal to 2b, where b is the distance between the center of the ellipse and point B1.
Distancefocal: Distance between ellipse foci and is always equal to 2c.
Eccentricity: is the following reason:
ç
The
The following image illustrates some of the elements of the Ellipse and the lengths that represent measures "a", "b" and "c", in which the relationship of Pythagoras: a2 = b2 + c2.
Reduced Ellipse Equations
The first equation reduced of the ellipse is used in the case where the focuses of this figure are on the x-axis and the center of the Ellipse is about the origin of the Cartesian plane:
x2 + y2 = 1
The2 B2
The second equationreduced gives Ellipse is used in the case where the foci of this figure are on the y axis and the center is on the origin of the Cartesian plane:
y2 + x2= 1
The2 B2
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-elipse.htm

