O greatest common divider (MDC) between two or more numbers is simply the largest numerical value that divides all those numbers. The divisors of a number are all those numeric values that divide that number and that leave no remainder in the division. Let's look at the number divisors 20 and 50.
D (20) = 1, 2, 4, 5, 10, 20
D(50) = 1, 2, 5, 10, 25, 50
The numbers 20 and 50 have the 2 it's the 10 as common dividers. But the greatest common divisor between 20 and 50 is the 10. We represent:
MDC (20, 50) = 10
Another way to find the MDC between two or more numbers is through successive divisions. We must perform the division of the largest by the smallest number to then do a new division, being that the number found in the rest will be the new divisor and the number that was in the divisor will now be the dividend. We repeat this process until we find zero remainder. Let's look at an example: if we want to find the greatest common divisor between 20 and 50, we should do “50 divided by 20”, which originates rest
10. We then do the division of 20 for 10 and we have an exact division. So as our last divider it was the 10, we say then that 10 is the greatest common divisor between 20 and 50. Let's see this process in the diagram below:
Through successive divisions, we find that the MDC (20, 50) = 10
Now let's look at the MDC (3, 4). First we made the division of 4 by 3. Making this division, we find remainder 1. Let's now divide the 3 for 1, which is an exact division, as it leaves zero remainder. We say then that MDC (3, 4) = 1. Whenever the greatest common divisor between two numbers is 1, we say that these numbers arecousins each other.
Do not stop now... There's more after the advertising ;)
Let's now look at the calculation to determine the greatest common divisor between 12 and 20:

Through successive divisions, we find that the greatest common divisor between 12 and 20 is the number 4
To determine the MDC (12, 20), we divide the 20 by 12, getting rest 08. So we do 12 divided by 8 and we get remainder 4. Finally, we do 8 divided by 4 and we found remainder 0, which assures us that MDC (12, 20) = 4.
To find the greatest common divisor between three or more numbers, we must repeat the same process between two of the numbers and then divide the third number by the found value. Let's think about calculating the greatest common divisor between numbers 4, 6 and 10. First, we perform the calculation of the greatest common divisor between 4 and 6. We easily verify that MDC (4, 6) = 2. So we make the third number divided by this 2 newly found. When dividing 10 for 2, we found zero remainder. We say, therefore, that the MDC (4, 6, 10) is 2.
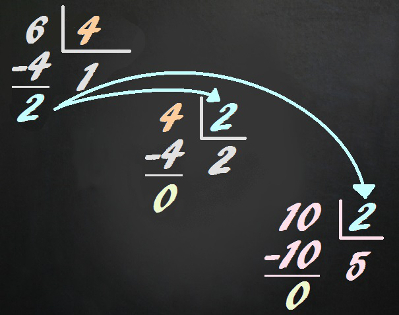
Using the process of successive divisions it is possible to find the MDC between three numbers or more
This rule can also be applied to resolve problems that involve the idea of the greatest common divisor.
By Amanda Gonçalves
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
RIBEIRO, Amanda Gonçalves. "Maximum Common Divisor (MDC)"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/maximo-divisor-comum.htm. Accessed on June 28, 2021.


