Angle between two vectors

Vectors are mathematical objects responsible for describing the trajectory of points. Many times, these points represent concrete objects in motion, which is studied in detail by Physics. When considering the forces involved in moving (in fact or potential) an object, Physics makes use of vectors to represent them. The angle these vectors form is a crucial part of the calculations, as a small variation in the angle may require more force to be applied to an object for it to start or stay in movement.

Vectors are geometrically represented by arrows, which are oriented straight lines. Thus, one end of the segment indicates the final position of the moved point, and the other end is unmarked, indicating that the movement started there. The endpoint location point is generally used to identify a vector that starts at the origin of a coordinate system. Considering the Cartesian plane as the coordinate system, a vector v, starting at point (0,0) and ending at point (a, b), is represented only as

vector v = (a, b). If the vector starts at another point, just move it to the appropriate place.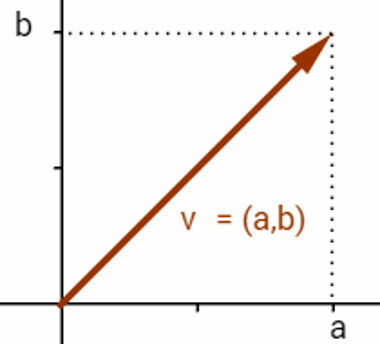

Vector in the Cartesian plane

Since these are oriented straight lines, it is possible to calculate their length, which is called the vector norm. The calculation of the norm of a vector is given in the same way as the distance between two points and is equivalent to calculating the modulus of a real number. In this way, the norm of the vector v = (a, b) is denoted by |v| and can be calculated as follows:

Do not stop now... There's more after the advertising ;)

Considering two vectors v = (a, b) and u = (a',b'), the domestic product among them is denoted by and is given by the following expression:

= a·a' + b·b'

The dot product between two vectors is also defined through the angle between them. This definition makes it possible to calculate the angle between two vectors.

Angle between two vectors

Thus, taking the same vectors v and u, the cosine of the angle θ between them is given by the following expression:

cosθ =
|v|·|u|

With these data, definitions and, in a way, formulas, it is possible to draw a strategy to calculate the angle between two vectors.

Given the vectors v = (2,2) and u = (0.2), we will calculate the angle between them. To do so, first calculate the norm of each vector and the product between these norms:

|v| = √(2² + 2²)
|v| = √(4 + 4)
|v| = √8

|u| = √(0² + 2²)
|u| = √(0 + 4)
|u| = √4

|v|·|u| = √8·√4
|v|·|u| = 4√2

Afterwards, calculate the inner product between v and u:

= 2·0 + 2·2
= 0 + 4
= 4

Finally, use the angle formula between vectors to calculate cosθ and a cosine values ​​table to find the value of θ.

cosθ =
|v|·|u|

cosθ =  4
4√2

cosθ =  4
4√2

cosθ =  2
√2

cosθ = √2
2

θ = 45°

By Luiz Paulo Moreira
Graduated in Mathematics

Would you like to reference this text in a school or academic work? Look:

SILVA, Luiz Paulo Moreira. "Angle between two vectors"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/Angulo-entre-dois-vetores.htm. Accessed on June 27, 2021.