Distance between two points: how to calculate

THE distance between two points is the first concept learned and one of the most important within the analytic geometry, considering that other concepts in this area derive from the idea of ​​distance between two points.

Read too: Three-point alignment condition

What is distance between two points?

the distance between two points depends on the locus where these points are located. For example, if two points are in a straight, the distance is given by the module of difference among them, see:

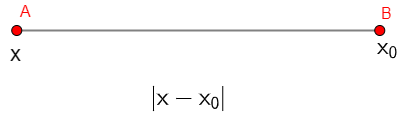
• Example

Imagine the following situation, on a trip, when we are going through a highway, we have some signs that mark the kilometer or position we are in at that moment. In an initial moment, we pass the km 12 sign, then we pass the 68 km sign.

In order to know how far we have gone, it is necessary to consider the two signs: km 12 and km 68. In this way, we calculate the modulus of the difference between these two points to obtain the distance covered, as follows:

|12 - 68|=

|68 - 12| =

56 km

The route developed by GPS is a practical application of the concept of distance between two points.

Distance between two points on the Cartesian plane

To determine the distance between two points on the Cartesian plane, it is necessary to perform the analysis both along the abscissa (x) and y-axis (y) directions. Check out:

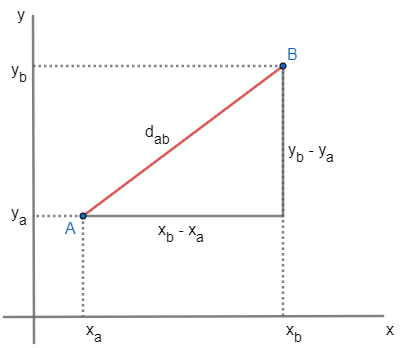
Note that in the distance between point A and B there is a variation both on the x-axis and on the y-axis, so the distance between the points must be given as a function of these variations.

Do not stop now... There's more after the advertising ;)

Also note that the distance between the points is the hypotenuse of the triangle formed. Also, applying the Pythagorean theorem and isolating the d side_ab, we have:

Read too: Generalities about straight line equations

Distance between two points formula

The distance between points A(x_They_The) and B(x_By_B) is defined by the length of the segment represented by d_ab and is measured by:

How to calculate the distance between two points?

To determine the distance between two points on the plane, simply substitute the coordinate values ​​of the points in the formula correctly. See below:

• Example

Calculate the distance between points P (-3, -11) and Q (2, 1).

Note that in the formula we must subtract the abscissa values ​​of each point and then square them, and the same must happen with the ordinate values. Thus:

solved exercises

question 1 – Knowing that the distance between points A and B is (root of 29) and that point A (1, y_a) belongs to axis O_x and B (-1, 5), determine y_a.

Solution:

Substituting the distance between two points in the formula, we have:

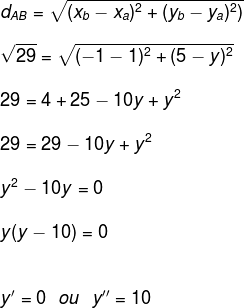
Since point A belongs to the X axis, then in fact y = 0.

Question 2 - (UFRGS) The distance between points A (-2, y) and B (6, 7) is 10. The value of y is:

to 1

b) 0

c) 1 or 13

d) -1 or 10

e) 2 or 12

Solution

Replacing the statement data, we have:

Solving the equation of the second degree, it follows that:

Answer: Alternative C

by Robson Luiz
Maths teacher

Would you like to reference this text in a school or academic work? Look:

LUIZ, Robson. "Distance between two points"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/distancia-entre-dois-pontos.htm. Accessed on June 27, 2021.

Three-point alignment condition

straight line, three-point alignment condition, point, slope, slope calculation, slope equality, parallel lines, coincident lines.