O barycenteris one of the notable points of triangle, which, in turn, is one of the simplest known polygons. This geometric figure is widely studied, and one of the points that deserves attention is the concept of barycenter.
We know as barycenter the triangle's center of gravity. To find it, it is necessary to determine its three medians, as well as the meeting point between them. When the triangle is represented in the Cartesian plane, to find the barycenter, just calculate the arithmetic mean between the values of x and y to find the ordered pair of the barycenter.
Read too: How are triangles classified?
What is the barycenter?

The triangle has important points, known as notable points, and the barycenter is one of them, along with the circumcenter, the incenter and the orthocenter. The barycenter is the triangle center of gravity and is represented by the letter G. He is located at the meeting of the medians of the triangle.
The median of a triangle is a segment that starts at a vertex and goes to the midpoint of the side opposite that vertex. In any triangle, it is possible to trace the three medians, each one starting from one of the vertices.
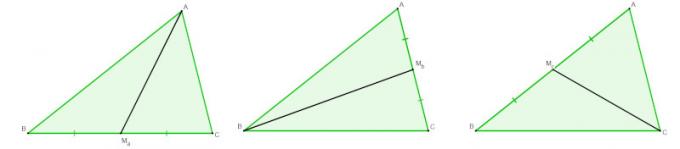
When we draw the three medians simultaneously, the three meet at a single point. This point, represented by G, is the barycenter.
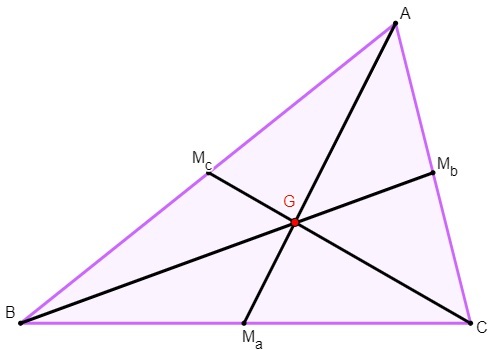
Barycenter properties
- Property 1: the barycenter is always an inner point of the triangle.
As the median is always an inner segment of the triangle, so is the barycenter, regardless of its shape.
- Property 2: the barycenter divides the median into two parts whose ratio is 1:2.
Analyzing the triangle represented above, we have that:
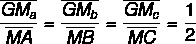
Do not stop now... There's more after the advertising ;)
How is the barycenter calculated?
When represented on the Cartesian plane, it is possible to find the coordinates of the triangle's barycenter. For this, let's calculate the arithmetic average of x values and also of y values.
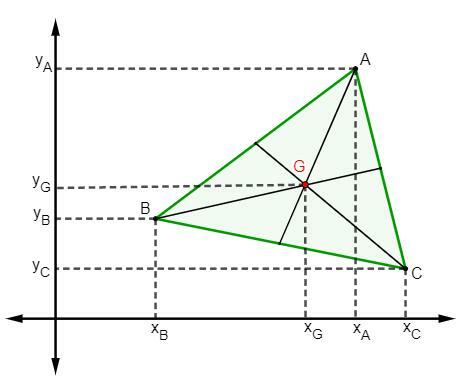
Note that the vertices are A(xTHEyTHE), B(xByB) and C (xÇyÇ), then, to find the coordinates of the barycenter G (xGyG), we use the formula:
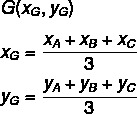
See too: Trigonometry in any triangle
solved exercises
Question 1 - We can state that the barycenter of the triangle whose vertices are the points A(2,1), B (-3, 5) and C (4,3) is the point:
A) G (1.3).
B) G (3.1).
C) G (3.3).
D) G(-2,-1).
E) G ( -1.3).
Resolution
Alternative A. To find the coordinates of the triangle's barycenter, let's calculate the arithmetic mean between the x values at points A, B and C and between the y values at the same points.
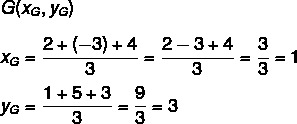
Thus, the barycenter is the G point (1,3).
Question 2 - In one city, three telephone towers will be installed to solve the problem with the network and signal failure for cell phones. It turns out that the positions of these towers were planned so that the center of the city coincides with the barycenter of the triangle with vertices at A, B and C, which are the locations of the towers. To choose the position of the towers, the city hall was defined as the origin of the axis, and the city center was located at point (1,-1). They made sure that the locations of points A and B would be A(12, -6), B(-4,-10). So what should the location of point C be?
A) (3.8)
B) (8,-13)
C) (3.8)
D) (-5, 13)
E) (-5, 8)
Resolution
Alternative D. We know that G is the city center location, which is the coordinate point (1,-1).
Let (x, y) be the coordinates of point C, then:
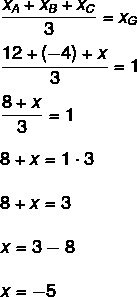
Also finding the y value:
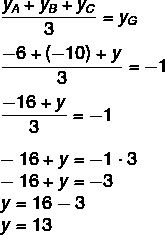
In this way we arrive at C (-5, 13).
By Raul Rodrigues de Oliveira
Maths teacher



