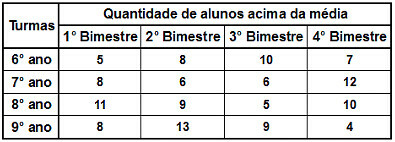
Within Statistics, there are several ways to analyze a set of data, depending on the need in each case. Imagine that a coach writes down the time spent by each of his athletes at each running workout and then observes that the The timing of some of your runners is showing considerable variation, which can result in defeat in a competition. official. In this case, it is interesting that the coach has some method to check the dispersion between the times of each athlete.
Of course Statistics has the right tool for this trainer! THE variance is dispersion measurethat allows to identify the distance in which the times of each athlete are from an average value. Suppose the coach recorded in a table the times of three athletes after completing the same course on five different days:

Before calculating the variance, it is necessary to find the arithmetic average (x) the times of each athlete. To do so, the coach made the following calculations:
João → xJ = 63 + 60 + 59 + 55 + 62 = 299 = 59.8 min.
5 5
Peter → xP = 54 + 59 + 60 + 57 + 61 = 291 = 58.2 min.
5 5
frames → xM = 60 + 63 + 58 + 62 + 55 = 298 = 59.6 min.
5 5
Now that the coach knows each athlete's average time, he can use the variance to obtain the distance of each race's periods from this average value. To calculate the variance for each corridor, the following calculation can be performed:
Var = (Day 1 - x)² + (day 2 - x)² + (day 3 - x)² + (day 4 - x)² + (day 5 - x)²
total days (5)
For each athlete, the coach calculated the variance:
João
Var (J) = (63 – 59,8)² + (60 – 59,8)² + (59 – 59,8)² + (55 – 59,8)² + (62 – 59,8)²
5
Do not stop now... There's more after the advertising ;)
Var (J) = 10,24 + 0,04 + 0,64 + 23,04 + 4,84
5
Var (J) = 38,8
5
Var (J) = 7.76 min
Peter
Var (P) = (54 – 58,2)² + (59 – 58,2)² + (60 – 58,2)² + (57 – 58,2)² + (61 – 58,2)²
5
Var (P) = 17,64 + 0,64 + 3,24 + 1,44 + 7,84
5
Var (P) = 30,8
5
Var (P) = 6.16 min
frames
Var (M) = (60 – 59,6)² + (63 – 59,6)² + (58 – 59,6)² + (62 – 59,6)² + (55 – 59,6)²
5
Var (M) = 0,16 + 11,56 + 2,56 + 5,76 + 21,16
5
Var (M) = 41,2
5
Var (M) = 8.24 min
According to the variance calculations, the athlete who presents the times more dispersed of the average is the Frames. Already Peter presented times closer to their average than the other runners.
How about we synthesize everything we've seen about variance with this example?
Given a set of data, variance is a measure of dispersion that shows how far each value in that set is from the central (average) value;
The smaller the variance, the closer the values are to the mean. Likewise, the larger it is, the farther the values are from the mean.
As in this example we calculate the variance of all the days when athletes trained under the supervision of the coach, we say that we calculated the population variance. Now imagine that the coach wants to analyze these athletes' times over the course of a year. It will be a lot of data, isn't it? In this case, it would be appropriate for the researcher to select only a few time records, a kind of sample. This calculation would be of a sample variance. The only difference between the sample variance and the calculation we performed is that the divisor is the number of days subtracted from 1:
Var. sample = (day to - x)² + (day b - x)² + (day c – x)² +... + (day n – x)²
(total days) - 1
By Amanda Gonçalves
Graduated in Mathematics