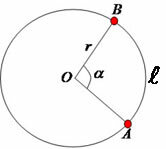
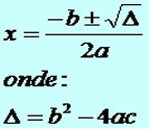Given a circle with center O, radius r and two points A and B belonging to the circle, we have that the distance between the marked points is an arc of a circle. The length of an arc is proportional to the measure of the central angle, the greater the angle, the greater the length of the arc; and the smaller the angle, the shorter the arc length.
To determine the length of a circle we use the following mathematical expression: C = 2*π*r. The complete turn in a circle is represented by 360º. Let's make a comparison between the circumference length in linear measure (ℓ) and angular measure (α), note:
linear |
angular |
2*π*r |
360º |
ℓ |
α Do not stop now... There's more after the advertising ;) |
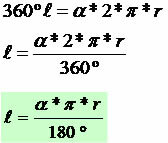
This expression can be used to determine the arc length of a circle of radius r and center angle α in degrees. In these cases use π = 3.14.
If the central angle is given in radians, we use the following expression: ℓ = α * r.
Example 1
Determine the length of an arc with a central angle equal to 30° contained in a circumference of radius 2 cm.
ℓ = α * π * r / 180º
ℓ = 30º * 3,14 * 2 / 180º
ℓ = 188,40 / 180
ℓ = 1.05 cm
The length of the bow will be 1.05 centimeters.
Example 2
The minute hand of a wall clock measures 10 cm. How much space will the hand travel after 30 minutes?
See the picture of the clock:

ℓ = α * π * r / 180º
ℓ = 180º * 3,14 * 10 / 180º
ℓ = 5652 / 180
ℓ = 31.4 cm
The space covered by the minute hand will be 31.4 centimeters.
Example 3
Determine the length of an arc with a center angle measuring π/3 contained in a circumference of 5 cm in radius.
ℓ = α * r
ℓ = π/3 * 5
ℓ = 5π/3
ℓ = 5*3,14 / 3
ℓ = 15,7 / 3
ℓ = 5.23 cm
Example 4
A 15 cm long pendulum swings between A and B at an angle of 15°. What is the length of the trajectory described by its extremity between A and B?
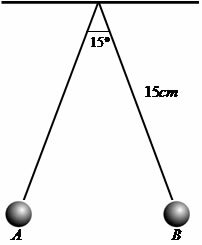
ℓ = α * π * r / 180º
ℓ = 15º * 3,14 * 15 / 180º
ℓ = 706,5 / 180
ℓ = 3.9 cm
The path length between A and B is 3.9 centimeters.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Trigonometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Length of an Arc"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/comprimento-um-arco.htm. Accessed on June 27, 2021.