The sum-to-product transformation formulas or prostapheresis (transformation) formulas are from very useful in factoring expressions such as sin x + sin y, cos x – cos y, sin x + cos x and others. To obtain the product transformations, we will use some formulas already known.
1. Transformation formula for sines
We will start from the formulas of the sine of the sum and the difference of two arcs to find an expression for sin x + sin y and for sin x – sin y.

Adding the two expressions member by member, we get:
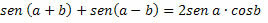
Subtracting the two expressions member by member, we get:
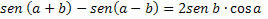
Making x = a + b and y = a - b, we will have:
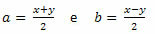
Follow that:

and
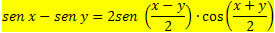
2. Transformation formula for cosines
Let's find an expression for cos x + cos y and for cos x – cos y.
We have to:
Do not stop now... There's more after the advertising ;)
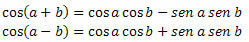
Adding the two equalities, member to member, we obtain:

Subtracting the two equalities, member by member, we obtain:

Making x = a + b and y = a - b, we get:


AND,
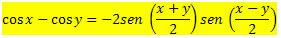
Example 1. Make the expression S = sin 37 into a productO + sin 23O.
Solution: We have that a = 37O and b = 23O. Soon,
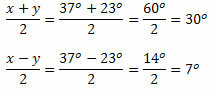
Thus,

Example 2. Factor the expression D = cos 5c – cos 3c.
Solution: We have that a = 5c and b = 3c. Soon,
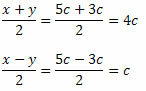
Thus,

By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
Trigonometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
RIGONATTO, Marcelo. "Sum-to-Product Transformation Formulas."; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/formulas-transformacao-soma-produto.htm. Accessed on June 27, 2021.