O Argand-Gauss plan it is made up of two axes: one vertical (known as the imaginary axis) and one horizontally (known as the real axis). It is possible geometrically represent complex numberswhich are in algebraic form.
Through this geometric representation, it is possible develop some concepts, such as the module and the argument of a complex number. Complex numbers are represented algebraically by z = a + bi, so they are represented by dots (a, b), which is called an affix.
Read too: Geometric representation of the sum of complex numbers
Geometric representation of complex numbers

The complex plane, also known as the Argand-Gauss plane, is nothing more than aCartesian plane for complex numbers. In the Argand-Gauss plane, it is possible to represent a complex number as a dot, known as an affix. With the development of the complex plan, there is the development of analytic geometry for complex numbers, which makes it possible to develop important concepts such as module and argument.
A complex number represented in its algebraic form is z = a+bi, on what The is the real part and B is the imaginary part. Therefore, complex numbers are represented as a dot (a, b). In the Argand-Gauss plane, the horizontal axis is the axis of the real part and the vertical axis is the axis of the imaginary part.
Do not stop now... There's more after the advertising ;)
Affix
O point on the plane representing a complex number it is also called an affix. There are three possible cases of representation: imaginary affixes, real affixes and pure imaginary affixes.
imaginary affixes
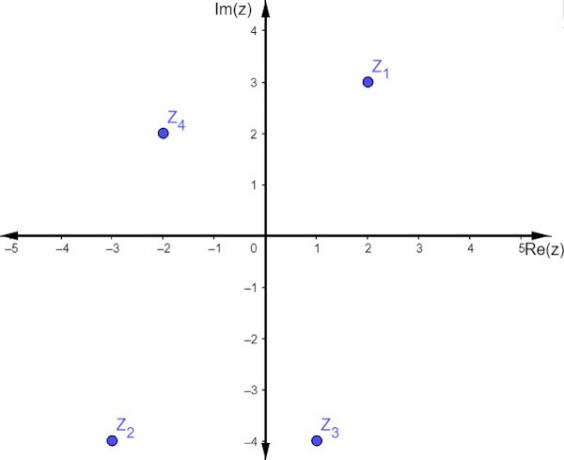
An affix is known as imaginary when the complex number has both a real part and imaginary part non-zero. In this case the affix is a point in any of the four quadrants, depending on the values of a, b and their respective signs.
Example:
See the representation of complex numbers z1 = 2 +3i, z2 = -3 - 4i, z3 = -2 + 2i and z4= 1 - 4i.
See too: Properties involving complex numbers
pure imaginary affixes
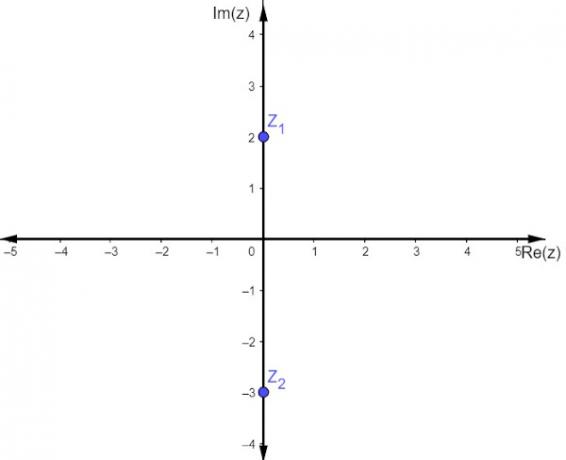
A complex number is known as a pure imaginary, when your real part equals zero, that is, z = bi. Note that in this case the first coordinate is always zero, so let's work with points of type (0, b). When marking in the Argand-Gauss plane, a pure imaginary affix always will be a point belonging to the imaginary axis, that is, to the vertical axis.
Example:
See the representation of complex numbers z1 = 2i and z2= -3i.
real affixes
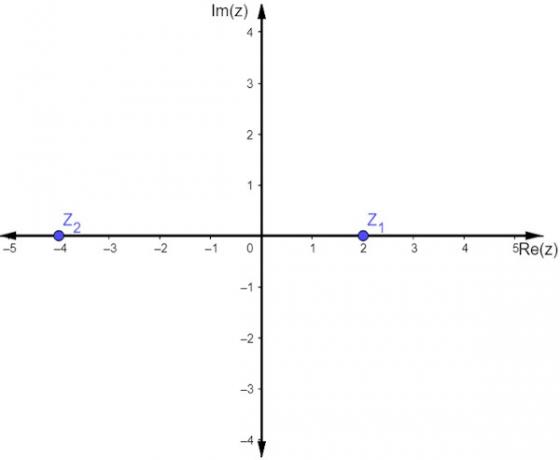
A complex number is classified as a real numberwhen your imaginary part equals zero, that is, z = a. In this case, the second coordinate is always zero, so we will work with points of type (a, 0), so the imaginary part is zero and the affixes are contained in the real axis of the complex plane.
Example:
See the representation of complex numbers z1 = 2 and z2 = -4.
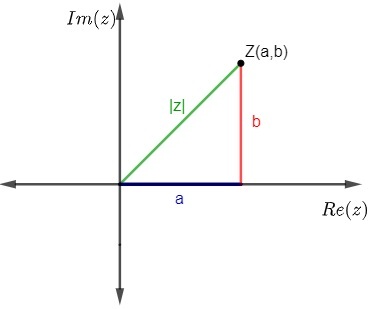
Complex number module
When representing a complex number, let P (a, b) be the affix of the complex number z = a + bi. We know as a complex number module a distance from point P to origin. The modulus of a complex number z is represented by |z|. To find the value of |z|, we use the Pythagorean theorem.
|z|² =a²+b²
We can also represent by:
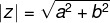
Example:
Find the modulus of the complex number z = 12 -5i.
|z|² = 12² + (-5)²
|z|² 144 + 25
|z|²= 169
|z|=√169
|z| =13
Also access: What are rational numbers?
complex number argument
We know how argument of a complex number O angle θ formed by the vector OP and the real axis. The argument of a number is represented by arg(z) = θ.
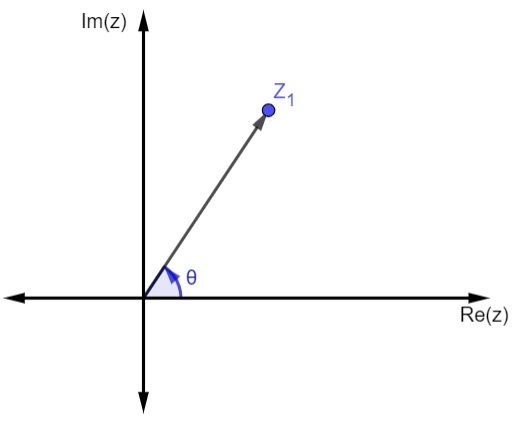
To find the angle, we use the trigonometric ratios sine and cosine.
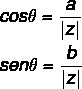
To find the value of the argument, knowing the sine and cosine, just consult the table of values for these trigonometric ratios. Usually, in college entrance exams on this topic, the argument is a remarkable angle.
Example:
Find the complex number argument z = 1 + i.
First let's calculate the modulus of z.
|z|² = 1² + 1²
|z|² = 1+1
|z|² = 2
|z| = √2
Knowing |z|, we can calculate the sine and cosine of the angle.

The angle that has sine and cosine with the values found is 45º.
solved exercises
Question 1 - What is the argument of the complex number z = √3+ i ?
A) 30th
B) 45th
C) 60th
D) 90º
E) 120th
Resolution
Alternative C.
We know that a = √3 and b = 1, so:
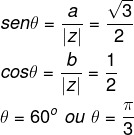
Question 2 - In the following complex plan, some numbers have been represented. Analyzing the plan, we can say that the points are representations of pure imaginary numbers:

A) M, N and I.
B) P and I.
C) L and G.
D) O, I, G.
E) K, J and L.
Resolution
Alternative B.
To identify a pure imaginary number in the complex plane, it is necessary that it be on top of the vertical axis, which, in this case, are points P and I.
By Raul Rodrigues de Oliveira
Maths teacher