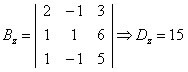Triangles have a very interesting particular property concerning the sum of their internal angles. This property guarantees that in any triangle, the sum of the measurements of the three interior angles equals 180 degrees.
To verify this statement, consider any triangle ABC.
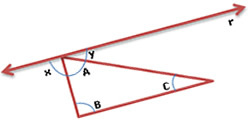
Also consider a line r, passing through point A and parallel to the side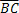 
(This line always exists and is unique!). As can be seen in the figure below, you can get the angles and so that x+y+A=180O.
Do not stop now... There's more after the advertising ;)
Knowing that the line r is the side (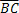) are parallel, the angles 
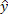and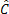
are internal alternates and therefore are congruent, this means that 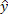=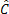. For the same reason, 
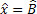. So, we have to:
A+x+y=A+B+C=180O
Thus, it is true that in every triangle the sum of the internal angles measures 180 degrees
by Franciely Guedes
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
GUEDES, Franciely Jesus. "Sum of the internal angles of a triangle";
Brazil School. Available in: https://brasilescola.uol.com.br/matematica/soma-dos-angulos-internos-um-triangulo.htm. Accessed on June 28, 2021.
