Solving the 3rd fundamental equation

Trigonometric equations are divided into three fundamental equations and each one of them works with a different function, and consequently has a different way of being solved.
The equation that represents the 3rd fundamental equation of trigonometry is tg x = tg a with a ≠ π/2 + k π. This equation means that if two arcs (angles) have the same tangent value, it means that they have the same distance from the center of the trigonometric cycle.

In the equation tg x = tg a, x is the unknown (which is the value of an angle) and the letter a is another angle that can be represented in degrees or radians and whose tangent is the same as x.
Solving this equation is done as follows:
x = a + k π (k 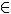Z)
And the solution to this resolution will be set up as follows:
S = {x 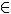R | x = a + kπ (k 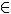Z)
See some examples of trigonometric equations that are solved using the 3rd fundamental equation method.
Example 1:
Give the solution set of the equation tg x = 

as tg  = , then:

tg x =  → tg x = 

x = π + k π (k 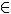Z)
S = {x

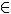R | x = π + kπ (k  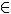Z) }
6
Example 2:
Solve the sec equation² x = (√3 – 1). tg x + √3 + 1, for 0 ≤ x ≤ π.
The +1 that is in the second member passes to the 1st member of the equality, so this equation can be written as follows:
sec ² x -1 = (√3 -1). tg x + √3
As sec2 x – 1 = tg² x, soon:
tg² x = (√3 -1) tg x + √3
Passing all terms from the 2nd member to the 1st member we will have:
tg² x - (√3 -1) tg x - √3 = 0
Substituting tg x = y, we have:
y² – (√3 -1) y - √3 = 0
Applying Bhaskara to this 2nd degree equation we will find two values ​​for y.
y’ = -1 and y" = √3
tg x = -1 → tg x = tg π → x = π
3 3
tg x = √3 → tg x = tg 3π → x = 3 π
4 4
S = { x 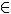 R | x = π + k π and x = 3 π (k Z)} 
3 4

Do not stop now... There's more after the advertising ;)

by Danielle de Miranda
Graduated in Mathematics

Would you like to reference this text in a school or academic work? Look:

RAMOS, Danielle de Miranda. "Solution of the 3rd fundamental equation"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/resolucao-3-equacao-fundamental.htm. Accessed on June 27, 2021.