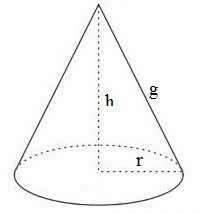
THE cone area it refers to the surface measure of this spatial geometric figure. Remember that the cone is a geometric solid with a circular base and a point, which is called the vertex.
Formulas: How to Calculate?
In the cone it is possible to calculate three areas:
Base Area
THEB =π.r2
Where:
THEB: base area
π (pi): 3.14
r: lightning
Side Area
THEthere = π.r.g
Where:
THEthere: side area
π (pi): 3.14
r: lightning
g: generator
Note: A generatrix corresponds to the measure of the side of the cone. Formed by any segment that has one end at the vertex and the other at the base, it is calculated by the formula: g2 = h2 + r2 (being H the height of the cone and r the Lightning)
Total area
At = π.r (g+r)
Where:
THEt: total area
π (pi): 3.14
r: lightning
g: generator
Cone Trunk Area
The so-called “trunk of the cone” corresponds to the part that contains the base of this figure. So, if we split the cone into two parts, we have one that contains the vertex, and one that contains the base.
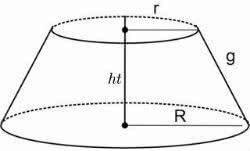
The latter is called the “trunk of the cone”. In relation to the area, it is possible to calculate:
Small Base Area (AB)
THEB = π.r2
Largest Base Area (AB)
THEB = π.R2
Side Area (Athere)
THEthere = π.g. (R + R)
Total Area (At)
THEt = AB + AB + Athere
Solved Exercises
1. What is the lateral area and total area of a straight circular cone that has a height of 8 cm and a base radius of 6 cm?
Resolution
First, we have to calculate the generatrix of this cone:
g = r2 + h2
g = √62 + 82
g = √36 + 64
g = √100
g = 10 cm
After that, we can calculate the lateral area using the formula:
THEthere = π.r.g
THEthere = π.6.10
THEthere = 60π cm2
By the formula of the total area, we have:
THEt = π.r (g+r)
At = π.6 (10+6)
At = 6π (16)
At = 96π cm2
We could solve it another way, that is, adding the areas of the side and base:
THEt = 60π + π.62
THEt = 96π cm2
2. Find the total area of the trunk of the cone that is 4 cm high, the larger base a 12 cm diameter circle, and the smaller base an 8 cm diameter circle.
Resolution
To find the total area of this trunk cone, it is necessary to find the areas of the largest base, the smallest and even the side.
Furthermore, it is important to remember the concept of diameter, which is twice the radius measurement (d = 2r). So, by the formulas we have:
Small Base Area
THEB = π.r2
THEB = π.42
THEB = 16π cm2
Major Base Area
THEB = π.R2
THEB = π.62
THEB = 36π cm2
Side Area
Before finding the lateral area, we have to find the measure of the generatrix of the figure:
g2 = (R - r)2 + h2
g2 = (6 – 4)2 + 42
g2 = 20
g = √20
g = 2√5
Once that's done, let's replace the values in the side area formula:
THEthere = π.g. (R + R)
THEthere = π. 2√5. (6 + 4)
THEthere = 20π√5 cm2
Total area
THEt = AB + AB + Athere
THEt = 36π + 16π + 20π√5
THEt = (52 + 20√5)π cm2
Entrance Exam Exercises with Feedback
1. (UECE) A straight circular cone whose height measurement is H, is sectioned, by a plane parallel to the base, into two parts: a cone whose height is h/5 and a cone trunk, as shown in the figure:
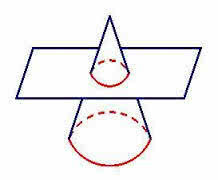
The ratio between the measurements of the volumes of the larger cone and the smaller cone is:
a) 15
b) 45
c) 90
d) 125
Alternative d: 125
2. (Mackenzie-SP) A perfume bottle, which has the shape of a straight circular cone of 1 cm and 3 cm radii, is completely full. Its contents are poured into a container that is shaped like a straight circular cylinder with a radius of 4 cm, as shown in the figure.
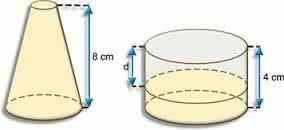
if d is the height of the unfilled part of the cylindrical vessel and, assuming π = 3, the value of d is:
a) 10/6
b) 6/11
c) 12/6
d) 13/6
e) 6/14
Alternative b: 6/11
3. (UFRN) An equilateral cone-shaped lamp is on a desk, so that when lit, it projects a circle of light on it (see figure below)

If the height of the lamp, in relation to the table, is H = 27 cm, the area of the illuminated circle, in cm2 will be equal to:
a) 225π
b) 243π
c) 250π
d) 270π
Alternative b: 243π
Read too:
- Cone
- Cone Volume
- pi number